题目内容
14. 我市某工厂设计了一款成本为20元/件的工艺品,现投放市场进行试销,其每天的销售量y(件)与销售单价x(元/件)之间满足的函数关系如图所示.
我市某工厂设计了一款成本为20元/件的工艺品,现投放市场进行试销,其每天的销售量y(件)与销售单价x(元/件)之间满足的函数关系如图所示.(1)求y与x之间的函数关系式;
(2)当该工艺品的销售单价定为多少元时,工厂每天获得的利润最大?最大利润是多少?
(3)根据工厂的实际,每天销售该工艺品的利润不得低于8000元,请结合二次函数的大致图象,求出该工艺品销售单价的范围.
分析 (1)利用待定系数法将(40,400),(60,200)代入可得函数关系式;
(2)根据利润=单件利润×销售量,列出函数关系式并配方可得最值;
(3)画出函数的大致图象,当W=8000时x=40或60,知40≤x≤60时,W≥8000.
解答 解:(1)根据题意,设y=kx+b,
将(40,400),(60,200)代入,
得:$\left\{\begin{array}{l}{40k+b=400}\\{60k+b=200}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-10}\\{b=800}\end{array}\right.$,
故y=-10x+800;
(2)设工厂每天获得的利润记为W,根据题意,
有,W=(x-20)(-10x+800)
=-10x2+1000x-16000
=-10(x-50)2+9000,
当x=50时,W取得最大值,最大值为9000;
答:该工艺品的销售单价定为50元时,工厂每天获得的利润最大,最大利润是9000元.
(3)该二次函数的大致图象如下图所示:
在W=-10x2+1000x-16000中,当W=8000时,即-10x2+1000x-16000=8000,
解得:x1=40,x2=60,
由函数图象可知,当该工艺品销售单价40≤x≤60时,每天销售该工艺品的利润不低于8000元.
点评 本题主要考查二次函数的实际应用能力,根据题意找到相等关系并列出函数关系式是解题关键.

练习册系列答案
相关题目
14.下列说法正确的是( )
| A. | 三个角对应相等的两个三角形全等 | |
| B. | 两个三角形全等,则对应边上的高对应相等 | |
| C. | 周长和一个角对应相等的两个三角形全等 | |
| D. | 两个三角形全等,面积不一定相等 |
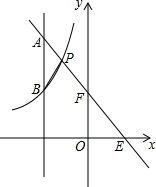 如图,直线l:y=-2x+2与双曲线y=$\frac{2k}{x}$(x<0)交于点P,只观察下图:
如图,直线l:y=-2x+2与双曲线y=$\frac{2k}{x}$(x<0)交于点P,只观察下图: 一张半径为R的半圆图纸沿它的一条弦折叠,使其弧与直径相切,如图所示,O为半圆圆心,如果切点分直径之比为3:2,则折痕长为$\frac{\sqrt{74}}{5}$R.
一张半径为R的半圆图纸沿它的一条弦折叠,使其弧与直径相切,如图所示,O为半圆圆心,如果切点分直径之比为3:2,则折痕长为$\frac{\sqrt{74}}{5}$R.
