题目内容
1.如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AD=2,BC=6,AB=3,E为BC边上一点,以BE为边作正方形BEFG,使正方形BEFG和梯形ABCD在BC的同侧.(1)①如图1,当正方形的顶点F恰好落在对角线AC上时,求BE的长;
②当正方形的顶点F恰好落在边CD上时,请直接写出BE的长为$\frac{18}{7}$;
(2)将图1中的正方形BEFG沿BC向右平移,记平移中的正方形BEFC为正方形MEFG,当点E与点C重合时停止平移.设平移的距离为t,正方形MEFG的边EF与AC交于点N,连接MD,MN,DN,是否存在这样的实数t,使△DMN是直角三角形?若存在,求出实数t的值;若不存在,请说明理由.

分析 (1)①如图1,首先设正方形BEFG的边长为x,易得△AGF∽△ABC,根据相似三角形的对应边成比例,即可求得BE的长;
②如图2,过点D作DH⊥BC于点H,交GF于点M,构建相似三角形:△DMF∽△FEC,结合该相似三角形的对应边成比例和正方形的性质解答即可;
(2)首先利用△NEC∽△ABC与勾股定理,求得MN,DN与MD的平方,然后分别从若∠DMN=90°,则DN2=MN2+MD2,若∠DMN=90°,则DM2=MN2+MD2,若∠MDN=90°,则MN2=MD2+DN2去分析,即可得到方程,解方程即可求得答案.
解答  解:(1)如图1,设正方形BEFG的边长为x,
解:(1)如图1,设正方形BEFG的边长为x,
则BE=FG=BG=x,
∵AB=3,BC=6,
∴AG=AB-BG=3-x,
∵GF∥BE,
∴△AGF∽△ABC,
∴$\frac{AG}{AB}$=$\frac{GF}{BC}$,
即$\frac{3-x}{3}$=$\frac{x}{6}$,
解得:x=2,
即BE=2; ①如图2,过点D作DH⊥BC于点H,交GF于点M,
①如图2,过点D作DH⊥BC于点H,交GF于点M,
∵∠DMF=∠FEC=90°,∠DFM=∠FCE,
∴△DMF∽△FEC,
则$\frac{DM}{EF}$=$\frac{MF}{CE}$,即$\frac{3-BE}{BE}$=$\frac{BE-2}{6-BE}$,
故BE=$\frac{18}{7}$.
故答案是:$\frac{18}{7}$.
(2)存在满足条件的t,
理由:如图3,过点D作DH⊥BC于H, 则BH=AD=2,DH=AB=3,
则BH=AD=2,DH=AB=3,
由题意得:BM=HE=t,HM=|t-2|,EC=4-t,
∵EF∥AB,
∴△NEC∽△ABC,
∴$\frac{NE}{AB}$=$\frac{EC}{BC}$,即$\frac{NE}{3}$=$\frac{4-t}{6}$,
∴NE=2-$\frac{1}{2}$t,
在Rt△MNE中,MN2=NE2+ME2=22+(2-$\frac{1}{2}$t)2=$\frac{1}{4}$t2-2t+8,
在Rt△DHM中,MD2=DH2+MH2=32+(t-2)2=t2-4t+13,
过点N作NN′⊥DH于N′,
则NN′=HE=t,N′H=NE=2-$\frac{1}{2}$t,
∴DN′=DH-N′H=3-(2-$\frac{1}{2}$t)=$\frac{1}{2}$t+1,
在Rt△DNN′中,DN2=DN′2+NN′2=$\frac{5}{4}$t2+t+1,
(Ⅰ)若∠DMN=90°,则DN2=MN2+MD2,
即$\frac{5}{4}$t2+t+1=($\frac{1}{4}$t2-2t+8)+(t2-4t+13),
解得:t=$\frac{20}{7}$,
(Ⅱ)若∠MND=90°,则MD2=MN2+DN2,
即t2-4t+13=($\frac{1}{4}$t2-2t+8)+($\frac{5}{4}$t2+t+1),
解得:t1=-3+$\sqrt{17}$,t2=-3-$\sqrt{17}$(舍去),
∴t=-3+$\sqrt{17}$;
(Ⅲ)若∠MDN=90°,则MN2=MD2+DN2,
即:$\frac{1}{4}$t2-2t+8=(t2-4t+13)+($\frac{5}{4}$t2+t+1),
此方程无解,
综上所述,当t=$\frac{20}{7}$或-3+$\sqrt{17}$时,△MDN是直角三角形.
点评 此题考查了相似三角形的判定与性质、正方形的性质、直角梯形的性质以及勾股定理等知识.此题难度较大,注意数形结合思想、方程思想与分类讨论思想的应用,注意辅助线的作法.

 如图,已知矩形ABCD∽矩形BCFE,AD=AE=1,则AB的长为$\frac{1+\sqrt{5}}{2}$.
如图,已知矩形ABCD∽矩形BCFE,AD=AE=1,则AB的长为$\frac{1+\sqrt{5}}{2}$.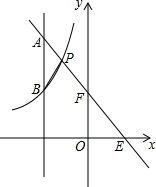 如图,直线l:y=-2x+2与双曲线y=$\frac{2k}{x}$(x<0)交于点P,只观察下图:
如图,直线l:y=-2x+2与双曲线y=$\frac{2k}{x}$(x<0)交于点P,只观察下图:
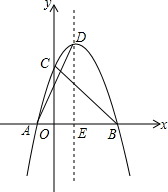 抛物线y=ax2+bx+3经过点A(-2,0),B(4,0),与y轴交于点C.
抛物线y=ax2+bx+3经过点A(-2,0),B(4,0),与y轴交于点C.
 如图,在△ABC中,点D、E、F分别在BC、AB、AC上.BD=CF,BE=CD,DG⊥EF于点G,且EG=FG.求证:AB=AC.
如图,在△ABC中,点D、E、F分别在BC、AB、AC上.BD=CF,BE=CD,DG⊥EF于点G,且EG=FG.求证:AB=AC.