题目内容
7. 如图,顺次连接正方形ABCD各边的中点得到四边形EFGH,如果正方形ABCD的面积为64cm2,估计四边形EFGH的每条边的长.(精确到0.01cm)
如图,顺次连接正方形ABCD各边的中点得到四边形EFGH,如果正方形ABCD的面积为64cm2,估计四边形EFGH的每条边的长.(精确到0.01cm)
分析 连接AC、BD,根据三角形中位线定理证明四边形EFGH是正方形,根据勾股定理求出正方形的一边长,得到答案.
解答 解: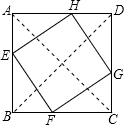 连接AC、BD,
连接AC、BD,
∵E、H分别为AB、AD的中点,
∴EH∥BD,EH=$\frac{1}{2}$BD,
∵F、G分别为BC、CD的中点,
∴FG∥BD,FG=$\frac{1}{2}$BD,
∴EH∥FG,EF=FG,
∴四边形EFGH是平行四边形,
∵AC=BD,
∴EF=EH,
∴四边形EFGH是菱形,
∵AC⊥BD,
∴∠E=90°,
∴四边形EFGH是正方形,
∵正方形ABCD的面积为64cm2,
∴AB=BC=8cm,
∴BE=BF=4cm,
∴EF=4$\sqrt{2}$cm≈5.66cm.
∴正方形EFGH的每条边的长约为5.66cm.
点评 本题考查的是三角形中位线定理和正方形的判定,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.

练习册系列答案
相关题目
18. 如图,平行四边形、矩形、菱形、正方形的包含关系可用如图表示,则图中阴影部分所表示的图形是( )
如图,平行四边形、矩形、菱形、正方形的包含关系可用如图表示,则图中阴影部分所表示的图形是( )
 如图,平行四边形、矩形、菱形、正方形的包含关系可用如图表示,则图中阴影部分所表示的图形是( )
如图,平行四边形、矩形、菱形、正方形的包含关系可用如图表示,则图中阴影部分所表示的图形是( )| A. | 矩形 | B. | 菱形 | C. | 矩形或菱形 | D. | 正方形 |
 如图,TQ切⊙O于点A,∠BAQ=60°,连接BO并延长与⊙O交于点C,与OA的延长线交于点T,若TC=2,求TA的长.
如图,TQ切⊙O于点A,∠BAQ=60°,连接BO并延长与⊙O交于点C,与OA的延长线交于点T,若TC=2,求TA的长.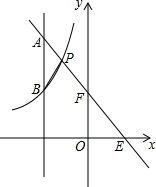 如图,直线l:y=-2x+2与双曲线y=$\frac{2k}{x}$(x<0)交于点P,只观察下图:
如图,直线l:y=-2x+2与双曲线y=$\frac{2k}{x}$(x<0)交于点P,只观察下图: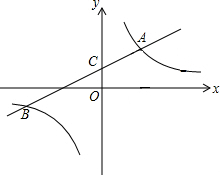 如图,一次函数y1=k1x+1与反比例函数y2=$\frac{k_2}{x}$的图象交于点A(3,2)和点B,与y轴交于点C.
如图,一次函数y1=k1x+1与反比例函数y2=$\frac{k_2}{x}$的图象交于点A(3,2)和点B,与y轴交于点C.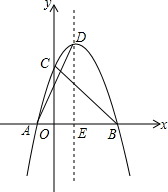 抛物线y=ax2+bx+3经过点A(-2,0),B(4,0),与y轴交于点C.
抛物线y=ax2+bx+3经过点A(-2,0),B(4,0),与y轴交于点C. 已知△ABC为等边三角形,延长BC到M,CA到N,使CM=AN,连BN交MA的延长线于Q,求∠BQM.
已知△ABC为等边三角形,延长BC到M,CA到N,使CM=AN,连BN交MA的延长线于Q,求∠BQM.