题目内容
9.有两个一元二次方程:M:ax2+bx+c=0;N:cx2+bx+a=0.其中a+c≠0,以下列四个结论中,错误的是( )| A. | 如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根 | |
| B. | 如果方程M有两根符号相同,那么方程N的两根符号也相同 | |
| C. | 如果5是方程M的一个根,那么$\frac{1}{5}$是方程N的一个根 | |
| D. | 如果方程M和方程N有一个相同的根,那么这个根必是x=1 |
分析 求出方程M:ax2+bx+c=0的判别式△1=b2-4ac,方程N:cx2+bx+a=0的判别式△2=b2-4ac,再根据判别式的意义、根与系数的关系以及方程的解的意义求解即可.
解答 解:A、如果方程M有两个不相等的实数根,那么△1=b2-4ac>0,所以△2=b2-4ac>0,所以方程N也有两个不相等的实数,结论正确,故本选项不符合题意;
B、如果方程M有两根符号相同,那么两根之积$\frac{c}{a}$>0,所以$\frac{a}{c}$>0,即方程N的两根之积>0,所以方程N的两根符号也相同,结论正确,故本选项不符合题意;
C、如果5是方程M的一个根,那么25a+5b+c=0,所以a+$\frac{1}{5}$b+$\frac{1}{25}$c=0,所以$\frac{1}{5}$是方程N的一个根,结论正确,故本选项不符合题意;
D、如果方程M和方程N有一个相同的根,那么ax2+bx+c=cx2+bx+a,整理得(a-c)x2=a-c,当a=c时,x为任意数;当a≠c时,x=±1.结论错误,故本选项符合题意;
故选D.
点评 本题考查了根的判别式,根与系数的关系以及一元二次方程的解的意义,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列说法正确的是( )
| A. | 中位数就是一组数据中最中间的一个数 | |
| B. | 7,8,8,9,9,10这组数据的众数是8 | |
| C. | 一组数据2,4,x,2,4,7的众数是2,则这组数据的平均数是3.5,中位数是3 | |
| D. | 一组数据的方差是这组数据的极差的平方 |

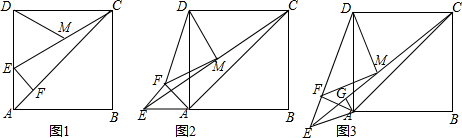
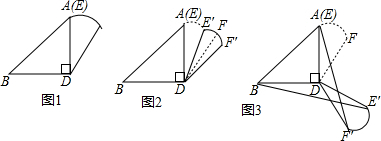
 如图所示,已知∠α和线段a,用尺规作一个三角形,使其一个内角等于∠α,夹这个角的两边分别为2a和a(保留作图痕迹,不写作法)
如图所示,已知∠α和线段a,用尺规作一个三角形,使其一个内角等于∠α,夹这个角的两边分别为2a和a(保留作图痕迹,不写作法)