题目内容
19.在数轴上作出表示1-$\sqrt{10}$的点.
分析 以数1的点为顶点,作出长为3宽为1的长方形,再以数1的点为顶点以长方形的对角线为半径画弧与表示1的点的左边相交,交点即为所求.
解答 解:如图所示,∵$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∴点A表示的数为1-$\sqrt{10}$.
点评 本题考查了勾股定理,实数与数轴,作出长为$\sqrt{10}$的线段是解题的关键.

练习册系列答案
相关题目
14.下列计算中,正确的是( )
| A. | 3x2•4x2=12x2 | B. | x3•x3=x5 | C. | (x4)2=x7 | D. | 2a•(-2ab2)2=8a3b4 |
4.两条直线被第三条直线所截.下列叙述正确的是( )
| A. | 同位角一定不相等 | B. | 内错角的对顶角-定相等 | ||
| C. | 同位角的邻补角一定相等 | D. | 两对同旁内角的和一定大于180° |
11.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2+$\sqrt{2}$=2$\sqrt{2}$ | C. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | D. | $\frac{\sqrt{4}}{2}$=2 |
8.下列说法正确的是( )
| A. | 64的立方根是±4 | B. | -$\frac{27}{64}$的立方根是$\frac{3}{4}$ | ||
| C. | -2是-8的立方根 | D. | -125的立方根是±5 |
9.有两个一元二次方程:M:ax2+bx+c=0;N:cx2+bx+a=0.其中a+c≠0,以下列四个结论中,错误的是( )
| A. | 如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根 | |
| B. | 如果方程M有两根符号相同,那么方程N的两根符号也相同 | |
| C. | 如果5是方程M的一个根,那么$\frac{1}{5}$是方程N的一个根 | |
| D. | 如果方程M和方程N有一个相同的根,那么这个根必是x=1 |
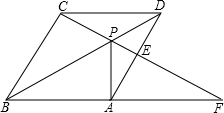 如图,点P是菱形ABCD对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于F,
如图,点P是菱形ABCD对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于F,