题目内容
17．（x-2a）（x+2a）（x2+4a2）=x4-16a4．分析 利用平方差公式的结构特征判断即可．
解答 解：（x-2a）（x+2a）（x2+4a2）=x4-16a4．
故答案为：（x2+4a2）．
点评 此题考查了平方差公式，熟练掌握平方差公式是解本题的关键．
练习册系列答案
相关题目
8．下列说法正确的是（ ）
| A． | 64的立方根是±4 | B． | -$\frac{27}{64}$的立方根是$\frac{3}{4}$ | ||
| C． | -2是-8的立方根 | D． | -125的立方根是±5 |
5．下列解方程正确的是（ ）
| A． | 由4x-6=2x+3移项得4x+2x=3-6 | |
| B． | 由$\frac{4}{7}x=5-\frac{x-1}{7}$，去分母得4x=5-x-1 | |
| C． | 由2（x+3）-3（x-1）=7，去括号得 2x+3-3x+1=7 | |
| D． | 由$\frac{x}{0.3}-0.5=x$得 $\frac{10x}{3}-\frac{1}{2}=x$ |
9．有两个一元二次方程：M：ax2+bx+c=0；N：cx2+bx+a=0．其中a+c≠0，以下列四个结论中，错误的是（ ）
| A． | 如果方程M有两个不相等的实数根，那么方程N也有两个不相等的实数根 | |
| B． | 如果方程M有两根符号相同，那么方程N的两根符号也相同 | |
| C． | 如果5是方程M的一个根，那么$\frac{1}{5}$是方程N的一个根 | |
| D． | 如果方程M和方程N有一个相同的根，那么这个根必是x=1 |
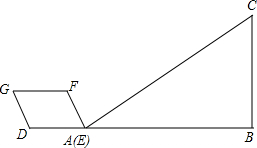平行四边形DEFG和Rt△ABC如图放置在同一直线上，点E与点A重合，AB=9，DE=3，DG=2，∠G=∠C=60°，∠B=90°．平行四边形DEFG从如图所示状态开始向右沿AB方向以每秒1个单位的速度平移，设运动的时间为t，直到点E与点B重合为止：
