题目内容
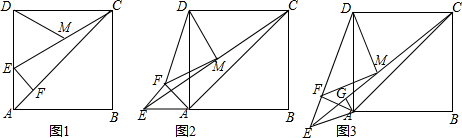
4.已知四边形ABCD是正方形,△AEF是等腰直角三角形,∠AFE=90°,点M是CE的中点,连接DM(1)如图1,当点E、F分别在AD、AC上时,若AD=4,EF=$\sqrt{2}$,求DM的长;
(2)如图2,当点E在BA延长线上时,连接DF,FM,求证:DM=FM,DM⊥FM;
(3)如图3,当点E不在BA延长线上且点F在DE上时,过点A作AG⊥EC,垂足为G,连接FM,试探究DM与FM的关系.
分析 (1)由等腰直角三角形的性质和正方形的性质直接求解;
(2)先判断△FEM≌△HCM,再判断出△DFA≌△DHC,最后得到△FDH是等腰直角三角形,即可;
(3)作出辅助线.同(2)的方法可证.
解答 解:(1)∵△AEF为等腰直角三角形,EF=$\sqrt{2}$,
∴AF=$\sqrt{2}$,AE=2,
∴DE=2,
由正方形ABCD得,DC=AD=4,
∴EC=2$\sqrt{5}$,
∵M为CE中点,
∴DM=$\frac{1}{2}$EC=$\sqrt{5}$,
(2)如图2,
延长FM交AC于H,连接DH,
∵∠FEA=∠CAB=45°,
∴EF∥AC,
∴∠FEM=∠MCH,
在△FEM和△HCM中,
$\left\{\begin{array}{l}{∠FEM=∠MCH}\\{EM=CM}\\{∠FME=∠CMH}\end{array}\right.$,
∴△FEM≌△HCM,
∴EF=CH=AF,FM=MH
∵AD=CD,
∴∠FAD=90°-45°=45°=∠DCH,
∴△DFA≌△DHC,
∴DF=DH,∠FDA=∠HDC,
∴∠FDH=90°,
∴△FDH是等腰直角三角形,
∵FM=HM.
∴DM⊥FM,DM=FM;
(3)如图3,
延长FM至H,使MH=FM,连接CH,
由(2)由△EFM≌△CHM,
∴EF=CH=AF,∠FEM=∠MCH,
∴CH?∥EF,
∴∠DCH+∠CDF=180°,
∴∠DCH+90°+∠ADF=180°,
∴∠DCH+∠ADF=90°,
∵∠ADF+∠FAD=90°,
∴∠DCH=∠FAD,
∵AD=CD,
∴△AFD≌△CHD,
∴DF=DH,∠ADF=∠CDH,
∴FDH=90°,
∴△FDH为等腰直角三角形,
∵FM=MH,
∴DM⊥FM,DM=$\frac{1}{2}$FH=FM.
点评 此题是四边形的综合题,主要考查了全等三角形的性质和判定,等腰直角三角形的直线和判定,解本题的关键是证明△FDH为等腰直角三角形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 3x2•4x2=12x2 | B. | x3•x3=x5 | C. | (x4)2=x7 | D. | 2a•(-2ab2)2=8a3b4 |
| A. | 一个锐角的余角是一个锐角 | B. | 任何一个角都有余角 | ||
| C. | 若∠1+∠2+∠3=90°,则∠1、∠2、∠3互余 | D. | 一个角的补角一定大于这个角 |
| A. | $\frac{x}{2}$-1=x,x=-2 | B. | 2-x=$\frac{1}{2}$+x,x=$\frac{3}{4}$ | C. | -$\frac{2}{3}$x=$\frac{3}{2}$,x=-$\frac{3}{4}$ | D. | -$\frac{x}{2}$+$\frac{2}{3}$=1,x=-$\frac{2}{3}$ |
| A. | 如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根 | |
| B. | 如果方程M有两根符号相同,那么方程N的两根符号也相同 | |
| C. | 如果5是方程M的一个根,那么$\frac{1}{5}$是方程N的一个根 | |
| D. | 如果方程M和方程N有一个相同的根,那么这个根必是x=1 |
 如图是小明进入中考复习阶段以来参加的10次物理水平测试成绩(满分70分)的统计图,那么关于这10次测试成绩,下列说法错误的是( )
如图是小明进入中考复习阶段以来参加的10次物理水平测试成绩(满分70分)的统计图,那么关于这10次测试成绩,下列说法错误的是( )| A. | 中位数是55 | B. | 众数是60 | C. | 方差是29 | D. | 平均数是54 |
| A. | 将原图形向x轴的正方向平移了6个单位,向y轴的正方向平移了5个单位 | |
| B. | 将原图形向x轴的负方向平移了6个单位,向y轴的正方向平移了5个单位 | |
| C. | 将原图形向x轴的负方向平移了6个单位,向y轴的负方向平移了5个单位 | |
| D. | 将原图形向x轴的正方向平移了6个单位,向y轴的负方向平移了5个单位 |
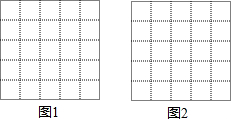 图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.