题目内容
14.已知Rt△DAB中,∠ADB=90°,扇形DEF中,∠EDF=30°,且DA=DB=DE,将Rt△ADB的边与扇形DEF的半径DE重合,拼接成图1所示的图形,现将扇形DEF绕点D按顺时针方向旋转,得到扇形DE′F′,设旋转角为α(0°<α<180°)(1)如图2,当0°<α<90°,且DF′∥AB时,求α;
(2)如图3,当α=120°,求证:AF′=BE′.
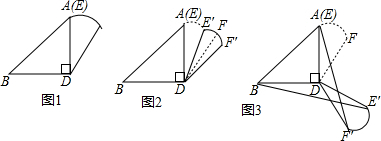
分析 (1)先利用直角三角形的性质,求出∠BAD,再由平行得到∠ADF′即可;
(2)先求出∠ADF′,再判断△ADF′≌△BDE′即可.
解答 解:(1)∵∠ADB=90°,DA=DB,
∴∠BAD=45°,
∵DF′∥AB,
∴∠ADF′=∠BAD=45°,
∴α=45°-30°=15°,
(2)∵α=120°,
∴∠ADE′=120°,
∴∠ADF′=120°+30°=150°,
∠BDE′=360°-90°-120°=150°,
∴∠ADF′=∠BDE′,
在△ADF′和△BDE′中,
$\left\{\begin{array}{l}{DA=DB}\\{∠ADF′=∠BDE′}\\{DE′=DF′}\end{array}\right.$,
∴△ADF′≌△BDE′,
∴AF′=BE′.
点评 此题是旋转性质题,主要考查了旋转角,全等三角形的判定和性质,解本题的关键是旋转角的计算.

练习册系列答案
相关题目
4.两条直线被第三条直线所截.下列叙述正确的是( )
| A. | 同位角一定不相等 | B. | 内错角的对顶角-定相等 | ||
| C. | 同位角的邻补角一定相等 | D. | 两对同旁内角的和一定大于180° |
5.下列解方程正确的是( )
| A. | 由4x-6=2x+3移项得4x+2x=3-6 | |
| B. | 由$\frac{4}{7}x=5-\frac{x-1}{7}$,去分母得4x=5-x-1 | |
| C. | 由2(x+3)-3(x-1)=7,去括号得 2x+3-3x+1=7 | |
| D. | 由$\frac{x}{0.3}-0.5=x$得 $\frac{10x}{3}-\frac{1}{2}=x$ |
9.有两个一元二次方程:M:ax2+bx+c=0;N:cx2+bx+a=0.其中a+c≠0,以下列四个结论中,错误的是( )
| A. | 如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根 | |
| B. | 如果方程M有两根符号相同,那么方程N的两根符号也相同 | |
| C. | 如果5是方程M的一个根,那么$\frac{1}{5}$是方程N的一个根 | |
| D. | 如果方程M和方程N有一个相同的根,那么这个根必是x=1 |
19.下列说法中错误的是( )
| A. | 9的算术平方根是3 | B. | 4的平方根是±2 | ||
| C. | 27的立方根是±3 | D. | 立方根等于-1的实数是-1 |
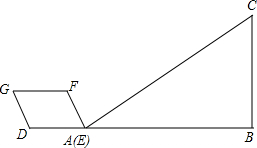 平行四边形DEFG和Rt△ABC如图放置在同一直线上,点E与点A重合,AB=9,DE=3,DG=2,∠G=∠C=60°,∠B=90°.平行四边形DEFG从如图所示状态开始向右沿AB方向以每秒1个单位的速度平移,设运动的时间为t,直到点E与点B重合为止:
平行四边形DEFG和Rt△ABC如图放置在同一直线上,点E与点A重合,AB=9,DE=3,DG=2,∠G=∠C=60°,∠B=90°.平行四边形DEFG从如图所示状态开始向右沿AB方向以每秒1个单位的速度平移,设运动的时间为t,直到点E与点B重合为止: 阅读下面材料:在数学课上,老师提出如下问题:尺规作图:
阅读下面材料:在数学课上,老师提出如下问题:尺规作图: