题目内容

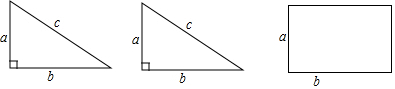
6．如图，有一张长方形纸板，在它的四角各剪去一个同样的正方形，然后将四周突出的部分折起，制成一个高为a的长方体形状的无盖纸盒．如果纸盒的容积为4a2b，底面长方形的一边长为b（b＜4a），求长方形纸板的面积．

分析 由长方体的容积除以高，再除以底面宽求出底面长，进而表示出长方形纸板的长与宽，表示出面积即可．

解答 解：根据题意得：4a2b÷ab=4a，
则长方形纸板的面积为（2a+b）（4a+2a）=12a2+6ab．

点评 此题考查了整式的混合运算，以及阴影部分面积的求法，熟练掌握运算法则是解本题的关键．

练习册系列答案
相关题目
14．若等腰三角形中有一个角等于40°，则这个等腰三角形顶角的度数为（　　）
A．40°B．100°C．40°或100°D．40°或70°
17．“吸烟有害健康！”国家为了加强对香烟产销的宏观管理，对销售香烟实行征收附加税政策，现在知道某品牌的香烟每条的市场价格为70元，不加收附加税时，每年销售110万条．若国家征收附加税，税率为x%（即每销售100元，征附加税x元），则每年的销售量将减少10x万条．要使每年对此项经营所收取附加税为168万元，问税率应确定为多少？
14．如图1，在△ABC中，tan∠A=$\frac{1}{2}$，∠B=45°，垂直于AB的直线与折线A-C-B相交于点E，垂足为点F，设AF=x，△AEF的面积为y，y与x之间的函数图象如图2，则当y=8时，x的值是4$\sqrt{2}$或6+2$\sqrt{5}$．
1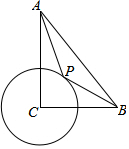．如图，在Rt△ABC中，∠ACB=90°，CB=4，CA=6，⊙C半径为2，P为圆上一动点，连结AP，BP，AP+$\frac{1}{2}$BP的最小值为（　　）
A．$\sqrt{37}$B．6C．2$\sqrt{17}$D．4
11．现有如图所示的三张卡片，两张是完全相同的直角三角形和一张长方形纸片，其中a＜b＜c．
（1）利用这三张卡片拼成各种形状不同的四边形，要求所拼成的四边形无缝隙且顶点重合，画出所拼成的四边形并计算它的周长；
（2）求周长最大的四边形与最小的四边形的差．
18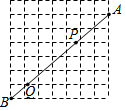．如图，在7×7的正方形网格中，连接两格点A，B，线段AB与其中两条网格线的交点为P，Q，则AP：PQ：QB的值为（　　）
A．2：3：1B．4：5：3C．2：4：1D．5：6：3
15．如图①，△ABC是正三角形，△BDC是顶角∠BDC=120°的等腰三角形，以D为顶点作一个60°角，角两边分别交AB，AC边于M，N两点，连接MN．
（I）探究：线段BM，MN，NC之间的关系，并加以证明．
提示：看到这个问题后，小明猜想：BM+NC=MN，并且通过延长AC到点E，使得CE=BM，连接DE，再证明三角形全等，请你按照小明的思路写出证明过程．
（Ⅱ）若点M是AB的延长线上的一点，N是CA的延长线上的点，其它条件不变，请你再探线段BM，MN，NC之间的关系，在图②中画出图形，并说明理由．
16．将一个等边三角形绕内角平分线的交点旋转一定角度后可以与原等边三角形重合，旋转的最小角度是（　　）
A．30°B．60°C．120°D．180°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网