题目内容
14.如图1,在△ABC中,tan∠A=$\frac{1}{2}$,∠B=45°,垂直于AB的直线与折线A-C-B相交于点E,垂足为点F,设AF=x,△AEF的面积为y,y与x之间的函数图象如图2,则当y=8时,x的值是4$\sqrt{2}$或6+2$\sqrt{5}$.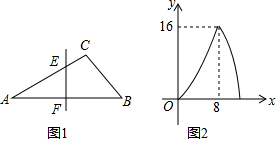
分析 当点E在AC上时,根据已知条件得到EF=$\frac{1}{2}$AF=$\frac{1}{2}$x,根据三角形的面积公式列方程即可得到结论;如图1,过C作CG⊥AB于G,由如图2知,当E与C,F与G重合时,△AEF的面积最大,此时,x=8,y=16,求得AG=8,CG=4,得到AB=12,当点E在BC上时,根据三角形的面积公式即可得到结论.
解答 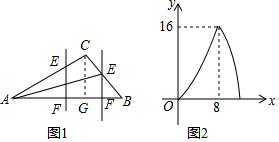 解:当点E在AC上时,
解:当点E在AC上时,
∵EF⊥AB,tan∠A=$\frac{1}{2}$,
∴EF=$\frac{1}{2}$AF=$\frac{1}{2}$x,
∴y=$\frac{1}{2}$×$\frac{1}{2}$x•x=$\frac{1}{4}$x2,
∴y=8时,即$\frac{1}{4}$x2=8,
解得x=4$\sqrt{2}$(负值舍去),
如图1,过C作CG⊥AB于G,
由如图2知,当E与C,F与G重合时,
△AEF的面积最大,此时,x=8,y=16,
即AG=8,CG=4,
∵∠B=45°,
∴BG=CG=4,
∴AB=12,
当点E在BC上时,
y=$\frac{1}{2}$•x•(12-x)=-$\frac{1}{2}$x2+6x,
∴y=8时,即-$\frac{1}{2}$x2+6x=8,
解得x=6+2$\sqrt{5}$(负值舍去),
∴当y=8时,x的值是4$\sqrt{2}$或6+2$\sqrt{5}$,
故答案为:4$\sqrt{2}$或6+2$\sqrt{5}$.
点评 本题考查了动点问题的函数图象,三角形的面积的计算,函数与图形的性质,掌握的识别图象是解题的关键.

练习册系列答案
相关题目
19.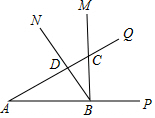 如图,∠PAQ=∠MBN=30°,∠MBN的顶点B在射线AP上,射线BM和射线BN分别交射线AQ于点C、D,当∠MBN绕点B转动时.若AB=2$\sqrt{3}$,则CA•CD的最小值是( )
如图,∠PAQ=∠MBN=30°,∠MBN的顶点B在射线AP上,射线BM和射线BN分别交射线AQ于点C、D,当∠MBN绕点B转动时.若AB=2$\sqrt{3}$,则CA•CD的最小值是( )
 如图,∠PAQ=∠MBN=30°,∠MBN的顶点B在射线AP上,射线BM和射线BN分别交射线AQ于点C、D,当∠MBN绕点B转动时.若AB=2$\sqrt{3}$,则CA•CD的最小值是( )
如图,∠PAQ=∠MBN=30°,∠MBN的顶点B在射线AP上,射线BM和射线BN分别交射线AQ于点C、D,当∠MBN绕点B转动时.若AB=2$\sqrt{3}$,则CA•CD的最小值是( )| A. | 3 | B. | $\sqrt{3}$ | C. | 4 | D. | 12 |
4.已知点P与点Q(0,2)关于坐标原点O成中心对称,那么点P的坐标是( )
| A. | (0,-2) | B. | (0,2) | C. | (2,0) | D. | (-2,0) |
 如图,有一张长方形纸板,在它的四角各剪去一个同样的正方形,然后将四周突出的部分折起,制成一个高为a的长方体形状的无盖纸盒.如果纸盒的容积为4a2b,底面长方形的一边长为b(b<4a),求长方形纸板的面积.
如图,有一张长方形纸板,在它的四角各剪去一个同样的正方形,然后将四周突出的部分折起,制成一个高为a的长方体形状的无盖纸盒.如果纸盒的容积为4a2b,底面长方形的一边长为b(b<4a),求长方形纸板的面积.