题目内容
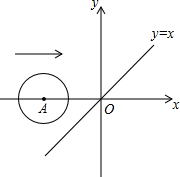 如图,在平面直角坐标系中,x轴上一点A从点(-3.1,0)出发沿x轴向右平移,当以A为圆心,半径为2的圆与函数y=x的图象相切时,点A的坐标是
如图,在平面直角坐标系中,x轴上一点A从点(-3.1,0)出发沿x轴向右平移,当以A为圆心,半径为2的圆与函数y=x的图象相切时,点A的坐标是考点:切线的性质,一次函数的性质
专题:计算题
分析:分类讨论:当⊙A在y轴左侧与直线y=x相切时,如图,作AB⊥直线y=x于点B,则AB=2,利用直线y=x为第一、三象限的角平分线得到∠AOB=45°,则△AOB为等腰直角三角形,所以OA=
AB=2
,于是得到A点坐标为(-2
,0);当⊙A运动到A′点,在y轴右侧与直线y=x相切时,如图,作A′B′⊥直线y=x于点B′,则A′B′=2,用同样的方法可求得A′点坐标为(2
,0),
| 2 |
| 2 |
| 2 |
| 2 |
解答:解: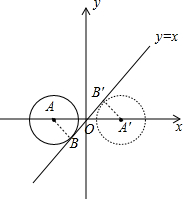 当⊙A在y轴左侧与直线y=x相切时,如图,
当⊙A在y轴左侧与直线y=x相切时,如图,
作AB⊥直线y=x于点B,则AB=2,
∵直线y=x为第一、三象限的角平分线,
∴∠AOB=45°,
∴△AOB为等腰直角三角形,
∴OA=
AB=2
,
∴A点坐标为(-2
,0);
当⊙A运动到A′点,在y轴右侧与直线y=x相切时,如图,作A′B′⊥直线y=x于点B′,则A′B′=2,
用同样的方法可求得A′点坐标为(2
,0),
综上所述,A点坐标为(-2
,0)或(2
,0).
故答案为(-2
,0)或(2
,0).
 当⊙A在y轴左侧与直线y=x相切时,如图,
当⊙A在y轴左侧与直线y=x相切时,如图,作AB⊥直线y=x于点B,则AB=2,
∵直线y=x为第一、三象限的角平分线,
∴∠AOB=45°,
∴△AOB为等腰直角三角形,
∴OA=
| 2 |
| 2 |
∴A点坐标为(-2
| 2 |
当⊙A运动到A′点,在y轴右侧与直线y=x相切时,如图,作A′B′⊥直线y=x于点B′,则A′B′=2,
用同样的方法可求得A′点坐标为(2
| 2 |
综上所述,A点坐标为(-2
| 2 |
| 2 |
故答案为(-2
| 2 |
| 2 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
 如图,已知△ABC是等边三角形,则∠BDC=( )
如图,已知△ABC是等边三角形,则∠BDC=( )| A、30° | B、60° |
| C、90° | D、120° |
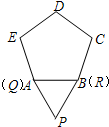 如图,将边长为1的等边△PQR沿着边长为1的正五边形ABCDE外部的边连续滚动(点Q、点R分别与点A、点B重合),当△PQR第一次回到原来的起始位置时(顶点位置与原来相同),点P所经过的路线长为( )
如图,将边长为1的等边△PQR沿着边长为1的正五边形ABCDE外部的边连续滚动(点Q、点R分别与点A、点B重合),当△PQR第一次回到原来的起始位置时(顶点位置与原来相同),点P所经过的路线长为( )A、
| ||
B、
| ||
| C、8π | ||
| D、16π |
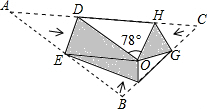 如图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,且EA与EB重合于线段EO,若∠DOH=78°,则∠FOG的度数为( )
如图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,且EA与EB重合于线段EO,若∠DOH=78°,则∠FOG的度数为( )| A、78° | B、102° |
| C、120° | D、112° |
设A(-1,y1)、B(1,y2)、C(3,y3)是抛物线y=-
(x-
)2+k上的三个点,则y1、y2、y3的大小关系是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、y1<y2<y3 |
| B、y2<y1<y3 |
| C、y3<y1<y2 |
| D、y2<y3<y1 |
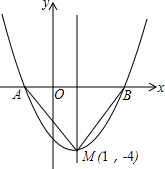 如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4)
如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4) 如图,抛物线y=x2-4x+3与x轴交于A、B两点,与y轴正半轴交于点C.在此抛物线上是否存在一点P,使直线OP与抛物线只有点P这个公共点?若存在请求出点P的坐标;若不存在,请说明理由.
如图,抛物线y=x2-4x+3与x轴交于A、B两点,与y轴正半轴交于点C.在此抛物线上是否存在一点P,使直线OP与抛物线只有点P这个公共点?若存在请求出点P的坐标;若不存在,请说明理由.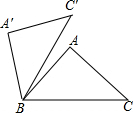 如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕点B逆时针旋转一定角度,点C′恰落在边BC上的高所在的直线上,则边BC在旋转过程中所扫过的面积为( )
如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕点B逆时针旋转一定角度,点C′恰落在边BC上的高所在的直线上,则边BC在旋转过程中所扫过的面积为( )