题目内容
已知a,b是整数,方程x2+ax+b=0的一个根为
,则a+b= .
6-2
|
考点:一元二次方程的解,二次根式的性质与化简
专题:
分析:方程的一个根是x=
,代入方程,由a,b是整数,列出关于a,b的方程组,求出a+b的值.
6-2
|
解答:解:把x=
代入方程x2+ax+b=0,得
6-2
+
a+b=0,
化简得:
(a-2)+b-a+6=0;
∵a,b是整数,
∴
,
解得:a=2,b=-4,a+b=-2,
故答案为-2.
6-2
|
6-2
| 5 |
6-2
|
化简得:
| 5 |
∵a,b是整数,
∴
|
解得:a=2,b=-4,a+b=-2,
故答案为-2.
点评:本题考查的是一元二次方程的解,把方程的解代入方程,根据二次根式的性质化简,得到关于a,b的方程组,求出a,b的值,即可求解.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
不等式组
的解集是( )
|
| A、x<1 | B、x>2 |
| C、1<x<2 | D、无解 |
 (1)如图所示,若AB=4cm,延长AB到C,使BC=3cm.如果点D是线段AB的中点,点E是线段AC的中点,求线段DE的长;
(1)如图所示,若AB=4cm,延长AB到C,使BC=3cm.如果点D是线段AB的中点,点E是线段AC的中点,求线段DE的长; 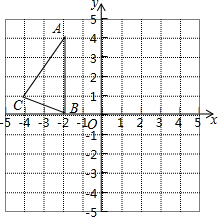 如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(-2,4)、(-2,0)、(-4,1),将△ABC绕原点O旋转180度得到△A1B1C1.平移△ABC得到△A2B2C2,使点A移动到点A2(0,2),结合所给的平面直角坐标系解答下列问题:
如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(-2,4)、(-2,0)、(-4,1),将△ABC绕原点O旋转180度得到△A1B1C1.平移△ABC得到△A2B2C2,使点A移动到点A2(0,2),结合所给的平面直角坐标系解答下列问题: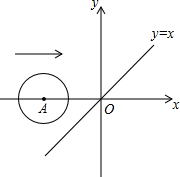 如图,在平面直角坐标系中,x轴上一点A从点(-3.1,0)出发沿x轴向右平移,当以A为圆心,半径为2的圆与函数y=x的图象相切时,点A的坐标是
如图,在平面直角坐标系中,x轴上一点A从点(-3.1,0)出发沿x轴向右平移,当以A为圆心,半径为2的圆与函数y=x的图象相切时,点A的坐标是