题目内容
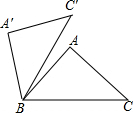 如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕点B逆时针旋转一定角度,点C′恰落在边BC上的高所在的直线上,则边BC在旋转过程中所扫过的面积为( )
如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕点B逆时针旋转一定角度,点C′恰落在边BC上的高所在的直线上,则边BC在旋转过程中所扫过的面积为( )| A、π | B、2π | C、3π | D、4π |
考点:扇形面积的计算,旋转的性质
专题:计算题
分析:利用∠A=90°,AB=AC=3可判断△ABC为等腰直角三角形,则BC=
AB=3
,BD=CD,再根据旋转的性质得BC′=BC=3
,所以BD=
BC′,利用含30度的直角三角形三边的关系得到∠BC′D=30°,则∠DBC′=60°,由于边BC在旋转过程中所扫过的部分为扇形,于是根据扇形的面积公式可计算出边BC在旋转过程中所扫过的面积.
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
解答:解:作高AD,则C′点在AD的反向延长线上,如图,
∵∠A=90°,AB=AC=3,
∴△ABC为等腰直角三角形,
∴BC=
AB=3
,BD=CD,
∵△ABC绕点B逆时针旋转一定角度,点C′恰落在边BC上的高所在的直线上,
∴BC′=BC=3
,
∴BD=
BC′,
∴∠BC′D=30°,
∴∠DBC′=60°,
∴边BC在旋转过程中所扫过的面积=
=3π.
故选C.
∵∠A=90°,AB=AC=3,
∴△ABC为等腰直角三角形,
∴BC=
| 2 |
| 2 |
∵△ABC绕点B逆时针旋转一定角度,点C′恰落在边BC上的高所在的直线上,
∴BC′=BC=3
| 2 |
∴BD=
| 1 |
| 2 |
∴∠BC′D=30°,
∴∠DBC′=60°,
∴边BC在旋转过程中所扫过的面积=
60•π•(3
| ||
| 360 |
故选C.
点评:本题考查了扇形面积计算公式:设圆心角是n°,圆的半径为R的扇形面积为S,则S扇形=
πR2或S扇形=
lR(其中l为扇形的弧长).也考查了旋转的性质.
| 360 |
| n |
| 1 |
| 2 |

练习册系列答案
相关题目
 如图,小镇A、B被一条河隔开,现在要在河上架设一座桥MN,桥架在何处可以使从A到B的路线最短?注意:桥必须与河垂直.
如图,小镇A、B被一条河隔开,现在要在河上架设一座桥MN,桥架在何处可以使从A到B的路线最短?注意:桥必须与河垂直.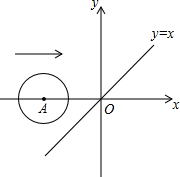 如图,在平面直角坐标系中,x轴上一点A从点(-3.1,0)出发沿x轴向右平移,当以A为圆心,半径为2的圆与函数y=x的图象相切时,点A的坐标是
如图,在平面直角坐标系中,x轴上一点A从点(-3.1,0)出发沿x轴向右平移,当以A为圆心,半径为2的圆与函数y=x的图象相切时,点A的坐标是 用一些长短相同的小木棍按图所示的方式,连续摆正方形或六边形,要求每两个相邻的图形只有一条公共边.
用一些长短相同的小木棍按图所示的方式,连续摆正方形或六边形,要求每两个相邻的图形只有一条公共边.
 如图,BE、DF是甲、乙两人在路灯下形成的影子,请在图中画出灯泡的位置.
如图,BE、DF是甲、乙两人在路灯下形成的影子,请在图中画出灯泡的位置.