题目内容
设A(-1,y1)、B(1,y2)、C(3,y3)是抛物线y=-
(x-
)2+k上的三个点,则y1、y2、y3的大小关系是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、y1<y2<y3 |
| B、y2<y1<y3 |
| C、y3<y1<y2 |
| D、y2<y3<y1 |
考点:二次函数图象上点的坐标特征
专题:
分析:先确定x>
时,是减函数,再找出A(-1,y1)对应A′的坐标,即可判定y1、y2、y3的大小关系.
| 1 |
| 2 |
解答:解:∵此函数的对称轴为x=
,且开口向下,
∴x>
时,是减函数,
∵A(-1,y1)对应A′(2,y1),
∴y3<y1<y2,
故选:C.
| 1 |
| 2 |
∴x>
| 1 |
| 2 |
∵A(-1,y1)对应A′(2,y1),
∴y3<y1<y2,
故选:C.
点评:本题主要考查了二次函数图象上点的坐标特征,解题的关键是确定函数的增减性质及A′的坐标.

练习册系列答案
相关题目
适合下列条件的△ABC中,直角三角形的个数为( )
①∠A:∠B:∠C=1:2:3;②a=6,b=6,∠A=45°;③∠A=32°,∠B=58°;④a=7,b=24,c=25;⑤a=2,b=2,c=4.
①∠A:∠B:∠C=1:2:3;②a=6,b=6,∠A=45°;③∠A=32°,∠B=58°;④a=7,b=24,c=25;⑤a=2,b=2,c=4.
| A、2个 | B、3个 | C、4个 | D、5个 |
若方程(m-3)x|m|-2=3yn+1+4是二元一次方程,则m,n的值分别为( )
| A、2,-1 | B、-3,0 |
| C、3,0 | D、±3,0 |
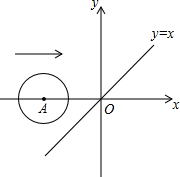 如图,在平面直角坐标系中,x轴上一点A从点(-3.1,0)出发沿x轴向右平移,当以A为圆心,半径为2的圆与函数y=x的图象相切时,点A的坐标是
如图,在平面直角坐标系中,x轴上一点A从点(-3.1,0)出发沿x轴向右平移,当以A为圆心,半径为2的圆与函数y=x的图象相切时,点A的坐标是 如图,BE、DF是甲、乙两人在路灯下形成的影子,请在图中画出灯泡的位置.
如图,BE、DF是甲、乙两人在路灯下形成的影子,请在图中画出灯泡的位置.