题目内容
 如图,抛物线y=x2-4x+3与x轴交于A、B两点,与y轴正半轴交于点C.在此抛物线上是否存在一点P,使直线OP与抛物线只有点P这个公共点?若存在请求出点P的坐标;若不存在,请说明理由.
如图,抛物线y=x2-4x+3与x轴交于A、B两点,与y轴正半轴交于点C.在此抛物线上是否存在一点P,使直线OP与抛物线只有点P这个公共点?若存在请求出点P的坐标;若不存在,请说明理由.考点:抛物线与x轴的交点
专题:
分析:可设出直线OP的解析式为y=kx,联立直线和抛物线的解析式消去y,根据直线与抛物线只有一个交点可求得k的值,可求得交点P的坐标.
解答:解:
∵直线OP过原点,
∴可设直线OP的解析式为y=kx,
联立两函数解析式可得
,
消去y整理可得x2-(4+k)x+3=0,
∵直线OP与抛物线只有一个公共点,
∴方程x2-(4+k)x+3=0有两个相等的实数根,
∴△=0,即(4+k)2-4×3=0,解得k=±2
-4,
当k=2
-4时,x2-(4+k)x+3=0的根为x1=x2=
,此时y=kx=(2
-4)×
=6-4
,即P点坐标为(
,6-4
);
当k=-2
-4时,x2-(4+k)x+3=0的根为x1=x2=-
,此时y=kx=(2
-4)×(-
)=4
-6,即P点坐标为(
,4
-6);
综上可知存在满足条件的点P,其坐标为P点坐标为(
,6-4
)或(
,4
-6).
∵直线OP过原点,
∴可设直线OP的解析式为y=kx,
联立两函数解析式可得
|
消去y整理可得x2-(4+k)x+3=0,
∵直线OP与抛物线只有一个公共点,
∴方程x2-(4+k)x+3=0有两个相等的实数根,
∴△=0,即(4+k)2-4×3=0,解得k=±2
| 3 |
当k=2
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
当k=-2
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
综上可知存在满足条件的点P,其坐标为P点坐标为(
| 3 |
| 3 |
| 3 |
| 3 |
点评:本题主要考查函数图象的交点问题,求出直线OP的解析式是解题的关键,注意分类讨论.

练习册系列答案
相关题目
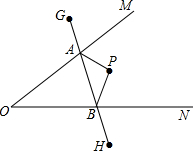 如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为10cm,求△PAB的周长为( )
如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为10cm,求△PAB的周长为( )| A、5cm | B、10cm |
| C、20cm | D、15cm |
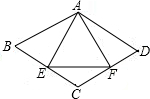 如图,在菱形ABCD内作一个等边△AEF,AE=AB.
如图,在菱形ABCD内作一个等边△AEF,AE=AB.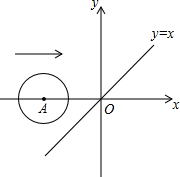 如图,在平面直角坐标系中,x轴上一点A从点(-3.1,0)出发沿x轴向右平移,当以A为圆心,半径为2的圆与函数y=x的图象相切时,点A的坐标是
如图,在平面直角坐标系中,x轴上一点A从点(-3.1,0)出发沿x轴向右平移,当以A为圆心,半径为2的圆与函数y=x的图象相切时,点A的坐标是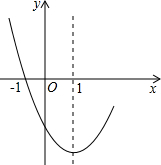 若二次函数y=x2-2x+c的部分图象如图所示,则关于x的方程x2-2x+c=0的两根为
若二次函数y=x2-2x+c的部分图象如图所示,则关于x的方程x2-2x+c=0的两根为 用一些长短相同的小木棍按图所示的方式,连续摆正方形或六边形,要求每两个相邻的图形只有一条公共边.
用一些长短相同的小木棍按图所示的方式,连续摆正方形或六边形,要求每两个相邻的图形只有一条公共边.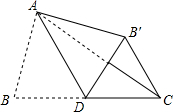 如图,在△ABC中,BC=5,AD为BC边上的中线,∠ADB=60°,将△ABD沿线段AD翻折,点B翻折到点B′的位置,连接CB′,则CB′的长为( )
如图,在△ABC中,BC=5,AD为BC边上的中线,∠ADB=60°,将△ABD沿线段AD翻折,点B翻折到点B′的位置,连接CB′,则CB′的长为( )