题目内容
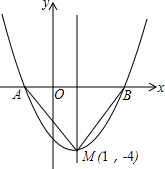 如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4)
如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4)(1)求出图象与x轴的交点A、B的坐标;
(2)在二次函数的图象上是否存在点P,使S△PAB=
| 5 |
| 4 |
考点:抛物线与x轴的交点,二次函数图象上点的坐标特征
专题:
分析:(1)由条件可先求得二次函数的解析式,再令y=0可求得A、B两点的坐标;
(2)由条件可先求得P点的纵坐标,再代入解析式可求得P点坐标.
(2)由条件可先求得P点的纵坐标,再代入解析式可求得P点坐标.
解答:解:(1)∵抛物线解析式为y=(x+m)2+k的顶点为M(1,-4)
∴y=(x-1)2-4 令y=0得(x-1)2-4=0解得x1=3,x2=-1
∴A(-1,0),B(3,0)
(2)∵△PAB与△MAB同底,且S△PAB=
S△MAB,
∴|yP|=
|yM|=
×4-5,即yP=±5
又∵点P在y=(x-1)2-4的图象上∴yP≥-4
∴yP=5,则(x-1)2-4=5,解得x1=4,x2=-2
∴存在合适的点P,坐标为(4,5)或(-2,5).
∴y=(x-1)2-4 令y=0得(x-1)2-4=0解得x1=3,x2=-1
∴A(-1,0),B(3,0)
(2)∵△PAB与△MAB同底,且S△PAB=
| 5 |
| 4 |
∴|yP|=
| 5 |
| 4 |
| 5 |
| 4 |
又∵点P在y=(x-1)2-4的图象上∴yP≥-4
∴yP=5,则(x-1)2-4=5,解得x1=4,x2=-2
∴存在合适的点P,坐标为(4,5)或(-2,5).
点评:本题主要考查待定系数法求函数解析式及二次函数图象点点的坐标,掌握二次函数顶点式y=a(x-h)2+k的顶点坐标为(h,k)是解题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
已知关于x的分式方程
=1,下列说法中正确的是( )
| 2m |
| x+6 |
| A、该方程的解是x=2m-6 |
| B、m<3时,该方程的解为负数 |
| C、m>3时,该方程的解为正数 |
| D、m≠3时,该方程无解 |
 如图,小镇A、B被一条河隔开,现在要在河上架设一座桥MN,桥架在何处可以使从A到B的路线最短?注意:桥必须与河垂直.
如图,小镇A、B被一条河隔开,现在要在河上架设一座桥MN,桥架在何处可以使从A到B的路线最短?注意:桥必须与河垂直. 如图,已知A(-4,n)、B(2,-4)是一次函数y=k1x+b1的图象和反比例函数y=
如图,已知A(-4,n)、B(2,-4)是一次函数y=k1x+b1的图象和反比例函数y=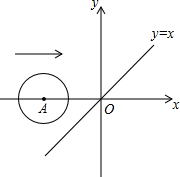 如图,在平面直角坐标系中,x轴上一点A从点(-3.1,0)出发沿x轴向右平移,当以A为圆心,半径为2的圆与函数y=x的图象相切时,点A的坐标是
如图,在平面直角坐标系中,x轴上一点A从点(-3.1,0)出发沿x轴向右平移,当以A为圆心,半径为2的圆与函数y=x的图象相切时,点A的坐标是