题目内容
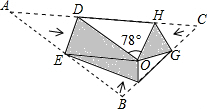 如图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,且EA与EB重合于线段EO,若∠DOH=78°,则∠FOG的度数为( )
如图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,且EA与EB重合于线段EO,若∠DOH=78°,则∠FOG的度数为( )| A、78° | B、102° |
| C、120° | D、112° |
考点:翻折变换(折叠问题)
专题:
分析:如图,证明∠DOE=∠A(设为α),∠EOF=∠B(设为β),∠GOH=∠C(设为γ);借助α+β+γ=180°,得到∠DOE+∠EOF+∠GOH=180°,即可解决问题.
解答: 解:如图,由题意得:
解:如图,由题意得:
∠DOE=∠A(设为α),∠EOF=∠B(设为β),
∠GOH=∠C(设为γ);
∵α+β+γ=180°,
∴∠DOE+∠EOF+∠GOH=180°;
∵∠DOH=78°,
∴∠FOG=360°-180°-78°=102°.
故选B.
 解:如图,由题意得:
解:如图,由题意得:∠DOE=∠A(设为α),∠EOF=∠B(设为β),
∠GOH=∠C(设为γ);
∵α+β+γ=180°,
∴∠DOE+∠EOF+∠GOH=180°;
∵∠DOH=78°,
∴∠FOG=360°-180°-78°=102°.
故选B.
点评:该题以三角形为载体,以翻折变换为方法,以考查三角形的内角和定理为核心构造而成;借助翻折变换的性质,灵活运用三角形的内角和定理来解题是关键.

练习册系列答案
相关题目
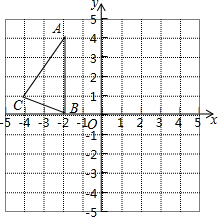 如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(-2,4)、(-2,0)、(-4,1),将△ABC绕原点O旋转180度得到△A1B1C1.平移△ABC得到△A2B2C2,使点A移动到点A2(0,2),结合所给的平面直角坐标系解答下列问题:
如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(-2,4)、(-2,0)、(-4,1),将△ABC绕原点O旋转180度得到△A1B1C1.平移△ABC得到△A2B2C2,使点A移动到点A2(0,2),结合所给的平面直角坐标系解答下列问题: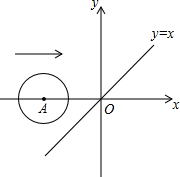 如图,在平面直角坐标系中,x轴上一点A从点(-3.1,0)出发沿x轴向右平移,当以A为圆心,半径为2的圆与函数y=x的图象相切时,点A的坐标是
如图,在平面直角坐标系中,x轴上一点A从点(-3.1,0)出发沿x轴向右平移,当以A为圆心,半径为2的圆与函数y=x的图象相切时,点A的坐标是 用一些长短相同的小木棍按图所示的方式,连续摆正方形或六边形,要求每两个相邻的图形只有一条公共边.
用一些长短相同的小木棍按图所示的方式,连续摆正方形或六边形,要求每两个相邻的图形只有一条公共边.
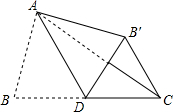 如图,在△ABC中,BC=5,AD为BC边上的中线,∠ADB=60°,将△ABD沿线段AD翻折,点B翻折到点B′的位置,连接CB′,则CB′的长为( )
如图,在△ABC中,BC=5,AD为BC边上的中线,∠ADB=60°,将△ABD沿线段AD翻折,点B翻折到点B′的位置,连接CB′,则CB′的长为( ) 如图,BE、DF是甲、乙两人在路灯下形成的影子,请在图中画出灯泡的位置.
如图,BE、DF是甲、乙两人在路灯下形成的影子,请在图中画出灯泡的位置.