题目内容
14.解下列不等式,并把它们的解集在数轴上表示出来:(1)4x-3≥2x+5
(2)$\frac{x-1}{2}$-$\frac{4x-3}{6}$>$\frac{1}{3}$.
分析 (1)根据不等式的性质,可以求得不等式的解集,并在数轴上表示出来;
(2)根据不等式的性质,可以求得不等式的解集,并在数轴上表示出来.
解答 解:(1)4x-3≥2x+5
移项及合并同类项,得
2x≥8
系数化为1,得
x≥4,
故原不等式的解集是x≥4,在数轴上表示如下所示,
(2)$\frac{x-1}{2}$-$\frac{4x-3}{6}$>$\frac{1}{3}$
两边同乘以6,得
3x-3-(4x-3)>2
去括号,得
3x-3-4x+3>2
移项及合并同类项,得
-x>2
系数化为1,得
x<-2
故原不等式的解集是x<-2,在数轴上表示如下所示,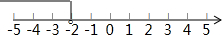
点评 本题考查解一元一次不等式\在数轴上表示不等式的解集,解题的关键是明确不等式的性质,会解一元一次不等式,并可以在数轴上表示出不等式的解集.

练习册系列答案
相关题目
4.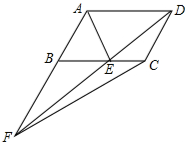 如图,在?ABCD中,点E在BC上,AE平分∠BAD,且AB=AE,连接DE并延长与AB的延长线交于点F,连接CF,若AB=1cm,则△CEF面积是$\frac{\sqrt{3}}{4}$cm2.
如图,在?ABCD中,点E在BC上,AE平分∠BAD,且AB=AE,连接DE并延长与AB的延长线交于点F,连接CF,若AB=1cm,则△CEF面积是$\frac{\sqrt{3}}{4}$cm2.
 如图,在?ABCD中,点E在BC上,AE平分∠BAD,且AB=AE,连接DE并延长与AB的延长线交于点F,连接CF,若AB=1cm,则△CEF面积是$\frac{\sqrt{3}}{4}$cm2.
如图,在?ABCD中,点E在BC上,AE平分∠BAD,且AB=AE,连接DE并延长与AB的延长线交于点F,连接CF,若AB=1cm,则△CEF面积是$\frac{\sqrt{3}}{4}$cm2.
2.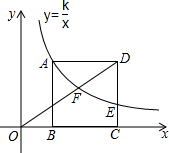 如图,在平面直角坐标系中,正方形ABCD的边BC在x轴正半轴上,点A、D在第一象限内,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点A交DC边于点E,交OD于点F,且CE=$\frac{1}{3}AB$,若点B的坐标为(1,0),则点F的坐标为( )
如图,在平面直角坐标系中,正方形ABCD的边BC在x轴正半轴上,点A、D在第一象限内,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点A交DC边于点E,交OD于点F,且CE=$\frac{1}{3}AB$,若点B的坐标为(1,0),则点F的坐标为( )
 如图,在平面直角坐标系中,正方形ABCD的边BC在x轴正半轴上,点A、D在第一象限内,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点A交DC边于点E,交OD于点F,且CE=$\frac{1}{3}AB$,若点B的坐标为(1,0),则点F的坐标为( )
如图,在平面直角坐标系中,正方形ABCD的边BC在x轴正半轴上,点A、D在第一象限内,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点A交DC边于点E,交OD于点F,且CE=$\frac{1}{3}AB$,若点B的坐标为(1,0),则点F的坐标为( )| A. | ($\frac{2\sqrt{3}}{3},\sqrt{3}$) | B. | ($\sqrt{3},\frac{2\sqrt{3}}{3}$) | C. | ($\frac{\sqrt{3}}{3},2\sqrt{3}$) | D. | (2$\sqrt{3},\frac{\sqrt{3}}{3}$) |
3.矩形ABCD的对角线AC,BD相交于点O,∠AOD=120°,AC=6,则△ABO的周长为( )
| A. | 18 | B. | 15 | C. | 12 | D. | 9 |
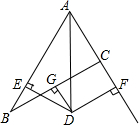 如图,在△ABC中,AB=8,AC=4,G为BC的中点,DG⊥BC交∠BAC的平分线AD于D,DE⊥AB于E,DF⊥AC于F交AC的延长线于F.
如图,在△ABC中,AB=8,AC=4,G为BC的中点,DG⊥BC交∠BAC的平分线AD于D,DE⊥AB于E,DF⊥AC于F交AC的延长线于F.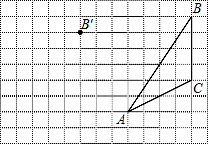 如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和直尺,完成下列各题:
如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和直尺,完成下列各题: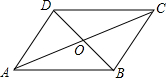 已知:?ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△DOA的周长长5cm,则这个平行四边形各边的长为$\frac{35}{2}$cm,$\frac{25}{2}$cm,$\frac{35}{2}$cm,$\frac{25}{2}$cm.
已知:?ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△DOA的周长长5cm,则这个平行四边形各边的长为$\frac{35}{2}$cm,$\frac{25}{2}$cm,$\frac{35}{2}$cm,$\frac{25}{2}$cm.