题目内容
5.不等式组 $\left\{\begin{array}{l}{x<2x+1}\\{3x-2(x-1)≤4}\end{array}\right.$的所有正整数解之和为3.分析 分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集,再将所有正整数解相加可得.
解答 解:解不等式x<2x+1,得:x>-1,
解不等式3x-2(x-1)≤4,得:x≤2,
∴不等式组的解集为:-1<x≤2,
则其所有正整数解之和为:1+2=3,
故答案为:3.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
16.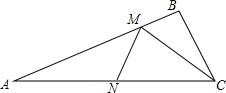 如图:△ABC中,AC=6,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )
如图:△ABC中,AC=6,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )
 如图:△ABC中,AC=6,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )
如图:△ABC中,AC=6,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3 |
13. 如图,在?ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
如图,在?ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
 如图,在?ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
如图,在?ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )| A. | $\frac{AF}{AB}$=$\frac{AE}{DE}$ | B. | $\frac{AF}{CD}$=$\frac{AE}{BC}$ | C. | $\frac{AF}{AB}=\frac{EF}{CE}$ | D. | $\frac{DE}{AE}=\frac{CE}{EF}$ |
10.若点(-2,y1),(-1,y2)(1,y3)在反比例函数y=$-\frac{2}{x}$的图象上,则下列结论正确的是( )
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y3>y2>y1 |
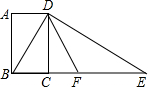 如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=3.设AB=x,AD=y,则x2+(y-3)2的值为9.
如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=3.设AB=x,AD=y,则x2+(y-3)2的值为9. 如图,将?ABCD的边AB延长至点E,使AB=BE,连接BD、DE、EC,DE交BC于点O.
如图,将?ABCD的边AB延长至点E,使AB=BE,连接BD、DE、EC,DE交BC于点O.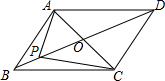 如图,已知四边形ABCD是平行四边形,点O为对角线AC、BD的交点
如图,已知四边形ABCD是平行四边形,点O为对角线AC、BD的交点