题目内容
9.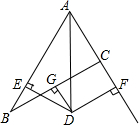 如图,在△ABC中,AB=8,AC=4,G为BC的中点,DG⊥BC交∠BAC的平分线AD于D,DE⊥AB于E,DF⊥AC于F交AC的延长线于F.
如图,在△ABC中,AB=8,AC=4,G为BC的中点,DG⊥BC交∠BAC的平分线AD于D,DE⊥AB于E,DF⊥AC于F交AC的延长线于F.(1)求证:BE=CF;
(2)求AE的长.
分析 (1)连接DB、DC,先由角平分线的性质就可以得出DE=DF,再证明△DBE≌△DCF就可以得出结论;
(2)由条件可以得出△ADE≌△ADF,就可以得出AE=AF,进而就可以求出结论.
解答 解:(1)如图,连接DB、DC,
∵DG⊥BC且平分BC,
∴DB=DC.
∵AD为∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF.∠AED=∠BED=∠ACD=∠DCF=90°
在Rt△DBE和Rt△DCF中
$\left\{\begin{array}{l}{DB=DC}\\{DE=DF}\end{array}\right.$
Rt△DBE≌Rt△DCF(HL),
∴BE=CF.
(2)在Rt△ADE和Rt△ADF中
$\left\{\begin{array}{l}{AD=AD}\\{DE=DF}\end{array}\right.$
∴Rt△ADE≌Rt△ADF(HL).
∴AE=AF.
∵AC+CF=AF,
∴AE=AC+CF.
∵AE=AB-BE,
∴AC+CF=AB-BE
∵AB=8,AC=4,
∴4+BE=8-BE,
∴BE=2,
∴AE=8-2=6.
点评 本题考查了角平分线的性质的运用,中垂线的性质的运用,全等三角形的判定与性质的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
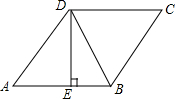 如图,在菱形ABCD中,已知DE⊥AB,AE:AD=3:5,BE=2,则菱形ABCD的面积是20.
如图,在菱形ABCD中,已知DE⊥AB,AE:AD=3:5,BE=2,则菱形ABCD的面积是20. 如图,将?ABCD的边AB延长至点E,使AB=BE,连接BD、DE、EC,DE交BC于点O.
如图,将?ABCD的边AB延长至点E,使AB=BE,连接BD、DE、EC,DE交BC于点O. 如图,在菱形ABCD中,对角线AC,BD相交于点O,E为AB的中点,且OE=2,则菱形ABCD的边长为4.
如图,在菱形ABCD中,对角线AC,BD相交于点O,E为AB的中点,且OE=2,则菱形ABCD的边长为4.