题目内容
4.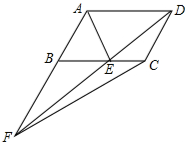 如图,在?ABCD中,点E在BC上,AE平分∠BAD,且AB=AE,连接DE并延长与AB的延长线交于点F,连接CF,若AB=1cm,则△CEF面积是$\frac{\sqrt{3}}{4}$cm2.
如图,在?ABCD中,点E在BC上,AE平分∠BAD,且AB=AE,连接DE并延长与AB的延长线交于点F,连接CF,若AB=1cm,则△CEF面积是$\frac{\sqrt{3}}{4}$cm2.
分析 由平行四边形的性质和角平分线的定义得出∠BAE=∠BEA,得出AB=BE=AE,所以△ABE是等边三角形,由AB的长,可求出△ABE的面积,再根据△FCD与△ABC等底(AB=CD)等高(AB与CD间的距离相等),可得S△FCD=S△ABC,又因为△AEC与△DEC同底等高,所以S△AEC=S△DEC,即S△ABE=S△CEF问题得解.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠EAD=∠AEB,
又∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴AB=BE,
∵AB=AE,
∴△ABE是等边三角形,
∵AB=1cm,
∴△ABE的面积=$\frac{1}{2}$×1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$cm2,
∵△FCD与△ABC等底(AB=CD)等高(AB与CD间的距离相等),
∴S△FCD=S△ABC,
又∵△AEC与△DEC同底等高,
∴S△AEC=S△DEC,
∴S△ABE=S△CEF=$\frac{\sqrt{3}}{4}$cm2.
故答案为:$\frac{\sqrt{3}}{4}$.
点评 此题考查了平行四边形的性质、等边三角形的判定与性质、三角形的面积关系,解题的关键是首先证明△ABE是等边三角形,求△CEF的面积转化为求△ABE的面积.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
16.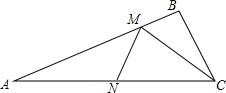 如图:△ABC中,AC=6,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )
如图:△ABC中,AC=6,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )
 如图:△ABC中,AC=6,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )
如图:△ABC中,AC=6,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3 |
13. 如图,在?ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
如图,在?ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
 如图,在?ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
如图,在?ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )| A. | $\frac{AF}{AB}$=$\frac{AE}{DE}$ | B. | $\frac{AF}{CD}$=$\frac{AE}{BC}$ | C. | $\frac{AF}{AB}=\frac{EF}{CE}$ | D. | $\frac{DE}{AE}=\frac{CE}{EF}$ |
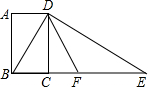 如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=3.设AB=x,AD=y,则x2+(y-3)2的值为9.
如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=3.设AB=x,AD=y,则x2+(y-3)2的值为9.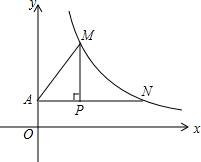 如图,点P的坐标为(2,$\frac{3}{2}$),过点P作x轴的平行线交y轴于点A,交双曲线y=$\frac{k}{x}$(x>0)于点N;作PM⊥AN交双曲线y=$\frac{k}{x}$(x>0)于点M,连接AM.已知PN=4.
如图,点P的坐标为(2,$\frac{3}{2}$),过点P作x轴的平行线交y轴于点A,交双曲线y=$\frac{k}{x}$(x>0)于点N;作PM⊥AN交双曲线y=$\frac{k}{x}$(x>0)于点M,连接AM.已知PN=4.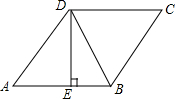 如图,在菱形ABCD中,已知DE⊥AB,AE:AD=3:5,BE=2,则菱形ABCD的面积是20.
如图,在菱形ABCD中,已知DE⊥AB,AE:AD=3:5,BE=2,则菱形ABCD的面积是20.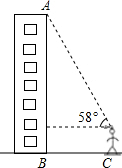 小明搬了新家,他想利用所学知识测量他家所在这栋楼的高度BA,如图所示,小明所站位置与这栋大楼的距离CB为30m,他仰望楼顶A处,仰角约为58°,已知小明身高为1.68m,请问这栋楼有多高?若每一层按照2.9m计算,你知道小明家所在的这栋楼共有多少层吗?(结果精确到0.1米)
小明搬了新家,他想利用所学知识测量他家所在这栋楼的高度BA,如图所示,小明所站位置与这栋大楼的距离CB为30m,他仰望楼顶A处,仰角约为58°,已知小明身高为1.68m,请问这栋楼有多高?若每一层按照2.9m计算,你知道小明家所在的这栋楼共有多少层吗?(结果精确到0.1米)