题目内容
19.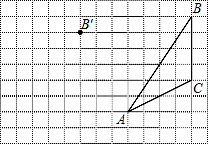 如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和直尺,完成下列各题:
如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和直尺,完成下列各题:(1)补全△A′B′C′;
(2)画出AB边上的中线CD;
(3)画出BC边上的高线AE;
(4)△A′B′C′的面积为8;
(5)点Q为格点(点Q不与点C重合),且△ABQ的面积等于△ABC的面积,在图中标出所有可能的Q点.
分析 (1)根据图形平移的性质画出图形即可;
(2)根据各点的特点找出线段AB的中点D,连接CD即可;
(3)过点A象BC的延长线作垂线,垂足为E即可;
(4)根据三角形的面积公式求出△A′B′C′的面积即可;
(5)过点A作AQ∥BC,使AQ=BC=4,分别过点C、Q作直线AB的平行线,两直线经过的格点即为点Q.
解答 解:(1)如图,△A′B′C′即为所求;
(2)如图,线段CD即为所求;
(3)如图,线段AE即为所求;
(4)S△A′B′C′=$\frac{1}{2}$×4×4=8.
故答案为:8;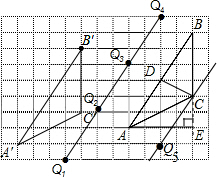
(5)如图所示,点Q1、Q2、Q3、Q4、Q5为所求点.
点评 本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
相关题目
10.若点(-2,y1),(-1,y2)(1,y3)在反比例函数y=$-\frac{2}{x}$的图象上,则下列结论正确的是( )
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y3>y2>y1 |
9.下列方程中,属于一元二次方程的是( )
| A. | $\frac{1}{{x}^{2}}+\frac{1}{x}-3=0$ | B. | ax2+bx+c=0 | C. | x2+5x=x2-3 | D. | x2-3x+2=0 |
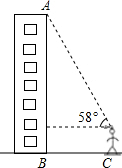 小明搬了新家,他想利用所学知识测量他家所在这栋楼的高度BA,如图所示,小明所站位置与这栋大楼的距离CB为30m,他仰望楼顶A处,仰角约为58°,已知小明身高为1.68m,请问这栋楼有多高?若每一层按照2.9m计算,你知道小明家所在的这栋楼共有多少层吗?(结果精确到0.1米)
小明搬了新家,他想利用所学知识测量他家所在这栋楼的高度BA,如图所示,小明所站位置与这栋大楼的距离CB为30m,他仰望楼顶A处,仰角约为58°,已知小明身高为1.68m,请问这栋楼有多高?若每一层按照2.9m计算,你知道小明家所在的这栋楼共有多少层吗?(结果精确到0.1米)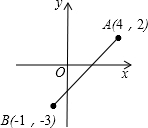 如图,在平面直角坐标系中,点A(4,2),B(-1,-3),P是x轴上的一点,Q是y轴上的一点,若以点A,B,P,Q四点为顶点的四边形是平行四边形,求点Q的坐标.
如图,在平面直角坐标系中,点A(4,2),B(-1,-3),P是x轴上的一点,Q是y轴上的一点,若以点A,B,P,Q四点为顶点的四边形是平行四边形,求点Q的坐标.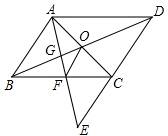 如图,在?ABCD中,F是边BC的中点,连接AF交DC的延长线于点E,AC,BD相交于点O,AF交BD于点G,连接OF,判断EC与OF的位置关系和大小关系,并证明你的结论.
如图,在?ABCD中,F是边BC的中点,连接AF交DC的延长线于点E,AC,BD相交于点O,AF交BD于点G,连接OF,判断EC与OF的位置关系和大小关系,并证明你的结论.