题目内容
6.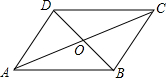 已知:?ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△DOA的周长长5cm,则这个平行四边形各边的长为$\frac{35}{2}$cm,$\frac{25}{2}$cm,$\frac{35}{2}$cm,$\frac{25}{2}$cm.
已知:?ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△DOA的周长长5cm,则这个平行四边形各边的长为$\frac{35}{2}$cm,$\frac{25}{2}$cm,$\frac{35}{2}$cm,$\frac{25}{2}$cm.
分析 平行四边形周长为60cm,即相邻两边之和为30,△AOB的周长比△DOA的周长长5cm,而AO为共用,OB=OD所以由题可知AB比AD长5,可列方程解答.
解答 解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC,
∵△AOB的周长比△DOA的周长长5cm,
∴AB-AD=5(cm),
又∵?ABCD的周长为60cm,
∴AB+AD=30cm,
则,AB=CD=$\frac{35}{2}$cm,AD=BC=$\frac{25}{2}$cm.
故答案为:$\frac{35}{2}$cm,$\frac{25}{2}$cm,$\frac{35}{2}$cm,$\frac{25}{2}$cm.
点评 此题主要考查了平行四边形的性质,关键是掌握平行四边形的对角线互相平分,对边相等.

练习册系列答案
相关题目
16.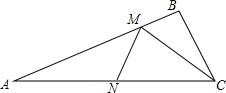 如图:△ABC中,AC=6,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )
如图:△ABC中,AC=6,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )
 如图:△ABC中,AC=6,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )
如图:△ABC中,AC=6,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3 |
16.下列多项式乘法中不能用平方差公式计算的是( )
| A. | (2x2y-1)(-2x2-1) | B. | (a3-b3)(b3-a3) | C. | (a+b)(a-b) | D. | (a2+b2)(b2-a2) |
 如图,在菱形ABCD中,对角线AC,BD相交于点O,E为AB的中点,且OE=2,则菱形ABCD的边长为4.
如图,在菱形ABCD中,对角线AC,BD相交于点O,E为AB的中点,且OE=2,则菱形ABCD的边长为4.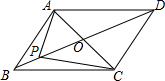 如图,已知四边形ABCD是平行四边形,点O为对角线AC、BD的交点
如图,已知四边形ABCD是平行四边形,点O为对角线AC、BD的交点