题目内容
2.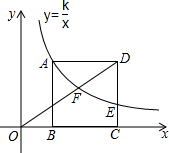 如图,在平面直角坐标系中,正方形ABCD的边BC在x轴正半轴上,点A、D在第一象限内,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点A交DC边于点E,交OD于点F,且CE=$\frac{1}{3}AB$,若点B的坐标为(1,0),则点F的坐标为( )
如图,在平面直角坐标系中,正方形ABCD的边BC在x轴正半轴上,点A、D在第一象限内,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点A交DC边于点E,交OD于点F,且CE=$\frac{1}{3}AB$,若点B的坐标为(1,0),则点F的坐标为( )| A. | ($\frac{2\sqrt{3}}{3},\sqrt{3}$) | B. | ($\sqrt{3},\frac{2\sqrt{3}}{3}$) | C. | ($\frac{\sqrt{3}}{3},2\sqrt{3}$) | D. | (2$\sqrt{3},\frac{\sqrt{3}}{3}$) |
分析 设正方形的边长为a,则A(1,a),E(a+1,$\frac{1}{3}$a),根据k=1•a=(a+1)•$\frac{1}{3}$a,求得a和k的值,然后得出D的坐标,根据待定系数法求得直线OD的解析式,与反比例函数解析式联立方程,解方程即可求得.
解答 解:设正方形的边长为a,
∵点B的坐标为(1,0),
∴OC=1+a,
∵CE=$\frac{1}{3}AB$,
∴CE=$\frac{1}{3}$a,
∴E(a+1,$\frac{1}{3}$a),
∵A(1,a),
∴1•a=(a+1)•$\frac{1}{3}$a,
解得a=2,
∴A(1,2),D(3,2),
把A(1,2)代入y=$\frac{k}{x}$求得k=2,
∴反比例函数y=$\frac{2}{x}$,
设直线OD的解析式为y=nx,
代入D(3,2)得,2=3n,解得n=$\frac{2}{3}$,
∴直线OD的解析式为y=$\frac{2}{3}$x,
解$\left\{\begin{array}{l}{y=\frac{2}{x}}\\{y=\frac{2}{3}x}\end{array}\right.$得$\left\{\begin{array}{l}{x=\sqrt{3}}\\{y=\frac{2\sqrt{3}}{3}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\sqrt{3}}\\{y=-\frac{2\sqrt{3}}{3}}\end{array}\right.$,
∴F($\sqrt{3}$,$\frac{2\sqrt{3}}{3}$),
故选B.
点评 本题考查了反比例函数图象上点的坐标特征,根据坐标特征得出k=1•a=(a+1)•$\frac{1}{3}$a,从而求得点的坐标和系数k是解题的关键.

 如图,在?ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
如图,在?ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )| A. | $\frac{AF}{AB}$=$\frac{AE}{DE}$ | B. | $\frac{AF}{CD}$=$\frac{AE}{BC}$ | C. | $\frac{AF}{AB}=\frac{EF}{CE}$ | D. | $\frac{DE}{AE}=\frac{CE}{EF}$ |
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y3>y2>y1 |
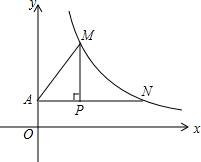 如图,点P的坐标为(2,$\frac{3}{2}$),过点P作x轴的平行线交y轴于点A,交双曲线y=$\frac{k}{x}$(x>0)于点N;作PM⊥AN交双曲线y=$\frac{k}{x}$(x>0)于点M,连接AM.已知PN=4.
如图,点P的坐标为(2,$\frac{3}{2}$),过点P作x轴的平行线交y轴于点A,交双曲线y=$\frac{k}{x}$(x>0)于点N;作PM⊥AN交双曲线y=$\frac{k}{x}$(x>0)于点M,连接AM.已知PN=4. 如图已知,OM平分∠AOB,点D,C分别在OM,OA上,∠COD=∠CDO,求证:CD∥OB.
如图已知,OM平分∠AOB,点D,C分别在OM,OA上,∠COD=∠CDO,求证:CD∥OB.