题目内容
8.阅读下列材料解决问题:材料:古希腊著名数学家 毕达哥拉斯发现把数1,3,6,10,15,21…这些数量的(石子),都可以排成三角形,则称像这样的数为三角形数.
把数 1,3,6,10,15,21…换一种方式排列,即
1=1
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5=15
…
从上面的排列方式看,把1,3,6,10,15,…叫做三角形数“名副其实”.
(1)设第一个三角形数为a1=1,第二个三角形数为a2=3,第三个三角形数为a3=6,请直接写出第n个三角形数为an的表达式(其中n为正整数).
(2)根据(1)的结论判断66是三角形数吗?若是请说出66是第几个三角形数?若不是请说明理由.
(3)根据(1)的结论判断所有三角形数的倒数之和T与2的大小关系并说明理由.
分析 (1)根据题意归纳总结得到一般性规律,写出即可;
(2)66是三角形数,理由为:根据得出的规律确定出原因即可;
(3)表示出的T表示后,利用拆项法整理判断即可.
解答 解:(1)根据题意得:an=$\frac{n(n+1)}{2}$(n为正整数);
(2)66是三角形数,理由如下:
当$\frac{n(n+1)}{2}$=66时,解得:n=11或n=-12(舍去),
则66是第11个三角形数;
(2)T=$\frac{1}{1}$+$\frac{1}{3}$+$\frac{1}{6}$+$\frac{1}{15}$+…+$\frac{2}{n(n+1)}$=$\frac{2}{1×2}$+$\frac{2}{2×3}$+$\frac{2}{3×4}$+$\frac{2}{4×5}$+…+$\frac{2}{n(n+1)}$=2(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$)=$\frac{2n}{n+1}$,
∵n为正整数,∴0<$\frac{n}{n+1}$<1,
则T<2.
点评 此题考查了规律型:数字的变化类,弄清题中的规律是解本题的关键.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
20.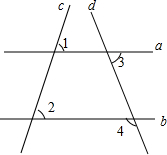 直线a、b、c、d的位置如图所示,如果∠1=80°,∠2=80°,∠3=70°,那么∠4等于( )
直线a、b、c、d的位置如图所示,如果∠1=80°,∠2=80°,∠3=70°,那么∠4等于( )
 直线a、b、c、d的位置如图所示,如果∠1=80°,∠2=80°,∠3=70°,那么∠4等于( )
直线a、b、c、d的位置如图所示,如果∠1=80°,∠2=80°,∠3=70°,那么∠4等于( )| A. | 70° | B. | 80° | C. | 100° | D. | 110° |
17.如图所示,四个三角形,能构成全等三角形的是( )


| A. | ②和③ | B. | ②和④ | C. | ①和② | D. | ③和④ |
 已知,如图,在△ABC中,AC>BC,B=45°,点D是AB的中点,CE⊥AB于点E.
已知,如图,在△ABC中,AC>BC,B=45°,点D是AB的中点,CE⊥AB于点E.