题目内容

17．如图所示，四个三角形，能构成全等三角形的是（　　）
A．②和③B．②和④C．①和②D．③和④

分析 先根据三角形内角和定理得到一个内角的度数，再根据ASA可证2个三角形全等，依此即可求解．

解答 解：①180°-60°-60°=60°，
②180°-70°-60°=50°，
③180°-70°-50°=60°，
④180°-60°-70°=50°，
根据ASA可证2个三角形全等是③和④．
故选：D．

点评 本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．

练习册系列答案
相关题目
20．下列各数：-（+3），|-4|，+6，-（-1.5）中，负数的个数是（　　）
A．1B．2C．3D．4
8．阅读下列材料解决问题：
材料：古希腊著名数学家 毕达哥拉斯发现把数1，3，6，10，15，21…这些数量的（石子），都可以排成三角形，则称像这样的数为三角形数．
把数 1，3，6，10，15，21…换一种方式排列，即
1=1
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5=15
…
从上面的排列方式看，把1，3，6，10，15，…叫做三角形数“名副其实”．
（1）设第一个三角形数为a1=1，第二个三角形数为a2=3，第三个三角形数为a3=6，请直接写出第n个三角形数为an的表达式（其中n为正整数）．
（2）根据（1）的结论判断66是三角形数吗？若是请说出66是第几个三角形数？若不是请说明理由．
（3）根据（1）的结论判断所有三角形数的倒数之和T与2的大小关系并说明理由．
5．（-$\frac{2}{3}$）+|0-5$\frac{1}{6}$|+|-4$\frac{5}{6}$|+（-9$\frac{1}{3}$）
12．解方程：x（x+1）=2x．
2．一条弦分圆为7：5两部分，这条弦所对的圆心角的度数150°．
9．下面的说法错误的是（　　）
A．0是最小的整数B．1是最小的正整数
C．0是最小的自然数D．自然数就是非负整数
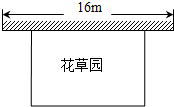6．某中学课外兴趣活动小组准备围建一个矩形花草园，其中一边靠墙，另外三边周长为30米的篱笆围成．已知墙长为16米（如图所示），设这个花草园垂直于墙的一边长为x米．
（1）若花草园的面积为100平方米，求x；
（2）若平行于墙的一边长不小于10米，这个花草园的面积有最大值和最小值吗？如果有，求出最大值和最小值；如果没有，请说明理由；
（3）当这个花草园的面积不小于88平方米时，直接写出x的取值范围．
7．2016年10月17日重庆南开中学将迎来80周年校庆，80年来，我校共培育了约72100名南开学子，72100这个数用科学记数法表示为7.21×104．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网