已知.如图.在△ABC中.AC＞BC.B=45°.点D是AB的中点.CE⊥AB于点E．求证:AC2=2(AD2+DE2)．题目和参考答案——青夏教育精英家教网——

题目内容

13．

已知，如图，在△ABC中，AC＞BC，B=45°，点D是AB的中点，CE⊥AB于点E．
求证：AC²=2（AD²+DE²）．

分析由已知条件得出BE=CE，根据勾股定理和完全平方公式进行计算，即可得出结论．

解答证明：∵D是AB的中点，
∴AD=BD，
∵CE⊥AB，∠B=45°，
∴BE=CE，
AC²=AE²+CE²=（AD+DE）²+（BD-DE）²=AD²+2AD•DE+DE²+BD²+2BD•DE+DE²=2AD²+2DE²=2（AD²+DE²）．

点评本题考查了勾股定理以及完全平方公式；熟练掌握勾股定理和完全平方公式是解决问题的关键．

练习册系列答案

优干线周周卷系列答案

轻松学习100分系列答案

精英新课堂系列答案

名师测控系列答案

名师课堂系列答案

名师学案系列答案

高效课堂导学案系列答案

培优新课堂系列答案

思维新观察系列答案

新领程系列答案

相关题目

16．用一个平面去截一个几何体，截面是三角形，这个几何体不可能是（　　）

17．仔细观察下列三组数：
第一组：1，-1，1，-1，1，-1，…
第二组：-2，4，-6，8，-10，12，…
第三组：1，4，9，16，25，36，…
（1）第三组的第100个数是第二组的第100个数的50倍．
（2）取每组数据的第10个数，计算这三个数的和．

由一些大小相同的小正方形搭成的几何体的俯视图，如图所示，其中正方形中的数字表示该位置上的小正方形的个数，请画出该几何体的主视图和左视图．

8．阅读下列材料解决问题：
材料：古希腊著名数学家毕达哥拉斯发现把数1，3，6，10，15，21…这些数量的（石子），都可以排成三角形，则称像这样的数为三角形数．
把数 1，3，6，10，15，21…换一种方式排列，即
1=1
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5=15
…
从上面的排列方式看，把1，3，6，10，15，…叫做三角形数“名副其实”．
（1）设第一个三角形数为a₁=1，第二个三角形数为a₂=3，第三个三角形数为a₃=6，请直接写出第n个三角形数为a_n的表达式（其中n为正整数）．
（2）根据（1）的结论判断66是三角形数吗？若是请说出66是第几个三角形数？若不是请说明理由．
（3）根据（1）的结论判断所有三角形数的倒数之和T与2的大小关系并说明理由．

18．一辆货车从超市出发，向东走了3km到达小彬家，继续走了1.5km到达小颖家，然后向西走了9.5km到达小明家，最后回到超市．
（1）小明家在超市的什么方向，距超市多远？以超市为原点，以向东的方向为正方向，用一个单位长度表示1km，你能在数轴上表示出小明家、小彬家、小颖家的位置吗？
（2）小明家距小彬家多远？
（3）火车一共行驶了多少千米？

5．（-$\frac{2}{3}$）+|0-5$\frac{1}{6}$|+|-4$\frac{5}{6}$|+（-9$\frac{1}{3}$）

2．一条弦分圆为7：5两部分，这条弦所对的圆心角的度数150°．

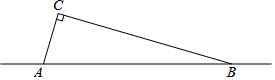在公路AB旁有一座山，现山脚的C处需要爆破，已知点C与公路上的停靠站A的距离是700米，与公路上另一停靠站B的距离为2400米，且CA垂直于CB，为了安全起见，爆破点C周围半径680米范围内不得进入．请问在爆破时，公路AB段是否因有危险而需要暂时封锁？