题目内容
9.当x为何值时,分式$\frac{2x-1}{x+1}$的值大于1?等于1?小于1?分析 根据题意列出不等式或者方程,再分类讨论.
解答 解:因为$\frac{2x-1}{x+1}$>1,
(1)当x+1>0时,
所以2x-1>x+1
解得x>2,
即当x>2时,分式$\frac{2x-1}{x+1}$的值大于1;
(2)当x+1<0时,
所以2x-1<x+1
解得x<2;
即当x<-1时,分式$\frac{2x-1}{x+1}$的值大于1;
综上当x>2或者x<-1时,分式$\frac{2x-1}{x+1}$的值大于1;
因为$\frac{2x-1}{x+1}$=1,
所以2x-1=x+1,
解得x=2.
当x=2时,x+1=3≠0,分式$\frac{2x-1}{x+1}$的值等于1;
因为$\frac{2x-1}{x+1}$<1,
(1)当x+1>0时,
所以2x-1<x+1
解得x<2,
即-1<x<2时,分式$\frac{2x-1}{x+1}$的值小于1;
(2)当x+1<0时,
所以2x-1>x+1
解得x>2;
所以分式$\frac{2x-1}{x+1}$的值不于1;
综上-1<x<2时,分式$\frac{2x-1}{x+1}$的值小于1.
点评 本题考查了分式方程和分式不等式,解决本题的关键需分类讨论.

练习册系列答案
 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
20.下列各数:-(+3),|-4|,+6,-(-1.5)中,负数的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 由一些大小相同的小正方形搭成的几何体的俯视图,如图所示,其中正方形中的数字表示该位置上的小正方形的个数,请画出该几何体的主视图和左视图.
由一些大小相同的小正方形搭成的几何体的俯视图,如图所示,其中正方形中的数字表示该位置上的小正方形的个数,请画出该几何体的主视图和左视图.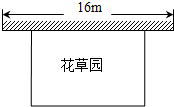 某中学课外兴趣活动小组准备围建一个矩形花草园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为16米(如图所示),设这个花草园垂直于墙的一边长为x米.
某中学课外兴趣活动小组准备围建一个矩形花草园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为16米(如图所示),设这个花草园垂直于墙的一边长为x米.