题目内容
18．计算：$\frac{{1}^{2}+{2}^{2}}{1×2}$+$\frac{{2}^{2}+{3}^{2}}{2×3}$+$\frac{{3}^{2}+{4}^{2}}{3×4}$+$\frac{{4}^{2}+{5}^{2}}{4×5}$+…+$\frac{201{4}^{2}+201{5}^{2}}{2014×2015}$．分析 把$\frac{{1}^{2}+{2}^{2}}{1×2}$+$\frac{{2}^{2}+{3}^{2}}{2×3}$+$\frac{{3}^{2}+{4}^{2}}{3×4}$+$\frac{{4}^{2}+{5}^{2}}{4×5}$+…+$\frac{201{4}^{2}+201{5}^{2}}{2014×2015}$变形为$\frac{1}{2}$+$\frac{2}{1}$+$\frac{2}{3}$+$\frac{3}{2}$+$\frac{3}{4}$+$\frac{4}{3}$+$\frac{4}{5}$+$\frac{5}{4}$+…+$\frac{2014}{2015}$+$\frac{2015}{2014}$，再根据加法交换律和结合律计算即可求解．
解答 解：$\frac{{1}^{2}+{2}^{2}}{1×2}$+$\frac{{2}^{2}+{3}^{2}}{2×3}$+$\frac{{3}^{2}+{4}^{2}}{3×4}$+$\frac{{4}^{2}+{5}^{2}}{4×5}$+…+$\frac{201{4}^{2}+201{5}^{2}}{2014×2015}$
=$\frac{1}{2}$+$\frac{2}{1}$+$\frac{2}{3}$+$\frac{3}{2}$+$\frac{3}{4}$+$\frac{4}{3}$+$\frac{4}{5}$+$\frac{5}{4}$+…+$\frac{2014}{2015}$+$\frac{2015}{2014}$
=$\frac{2}{1}$+（$\frac{1}{2}$+$\frac{3}{2}$）+（$\frac{2}{3}$+$\frac{4}{3}$）+（$\frac{3}{4}$+$\frac{5}{4}$）+…+（$\frac{2013}{2014}$+$\frac{2015}{2014}$）+$\frac{2014}{2015}$
=2×2014+$\frac{2014}{2015}$
=4028+$\frac{2014}{2015}$
=4028$\frac{2014}{2015}$．
点评 此题考查了有理数的混合运算，关键是把$\frac{{1}^{2}+{2}^{2}}{1×2}$+$\frac{{2}^{2}+{3}^{2}}{2×3}$+$\frac{{3}^{2}+{4}^{2}}{3×4}$+$\frac{{4}^{2}+{5}^{2}}{4×5}$+…+$\frac{201{4}^{2}+201{5}^{2}}{2014×2015}$变形为$\frac{1}{2}$+$\frac{2}{1}$+$\frac{2}{3}$+$\frac{3}{2}$+$\frac{3}{4}$+$\frac{4}{3}$+$\frac{4}{5}$+$\frac{5}{4}$+…+$\frac{2014}{2015}$+$\frac{2015}{2014}$计算．
| A． | 0是最小的整数 | B． | 1是最小的正整数 | ||
| C． | 0是最小的自然数 | D． | 自然数就是非负整数 |
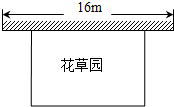某中学课外兴趣活动小组准备围建一个矩形花草园，其中一边靠墙，另外三边周长为30米的篱笆围成．已知墙长为16米（如图所示），设这个花草园垂直于墙的一边长为x米．
，那么加上卡片上的数字；如果抽到的卡片形如
，那么减去卡片上的数字；
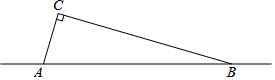在公路AB旁有一座山，现山脚的C处需要爆破，已知点C与公路上的停靠站A的距离是700米，与公路上另一停靠站B的距离为2400米，且CA垂直于CB，为了安全起见，爆破点C周围半径680米范围内不得进入．请问在爆破时，公路AB段是否因有危险而需要暂时封锁？