题目内容
3.在△ABC中,AB=13,AC=15,高AD=12,求△ABC的周长.分析 根据题意画出图形,再分AD在△ABC内与AD在△ABC外两种情况进行分类讨论.
解答 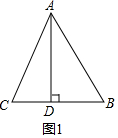 解:在Rt△ABD中BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5;
解:在Rt△ABD中BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5;
Rt△ACD中CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{1{5}^{2}-1{2}^{2}}$=9.
如图1,当AD在△ABC内时,BC=BD+CD=5+9=14,
△ABC的周长为42;
如图2,当AD在△ABC外时,BC=CD-BD=9-5=4,
△ABC的周长为32.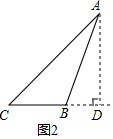
综上所述,△ABC的周长为42或32.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
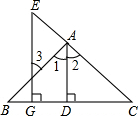 如图,已知AD⊥BC于D,EG⊥BC于G,AD平分∠BAC,
如图,已知AD⊥BC于D,EG⊥BC于G,AD平分∠BAC, ,那么加上卡片上的数字;如果抽到的卡片形如
,那么加上卡片上的数字;如果抽到的卡片形如 ,那么减去卡片上的数字;
,那么减去卡片上的数字;