题目内容
7．已知（2x-1）5=a5x5+a4x4+a3x3+a2x2+a1x+a0．求：（1）a0+a1+a2+a3+a4+a5的值．
（2）a0-a1+a2-a3+a4-a5的值．
（3）a0+a2+a4的值．
（4）a0的值．
分析 （1）直接利用x=1时代入原式求出答案；
（2）直接利用x=-1时代入原式求出答案；
（3）由（1）（2）得出a0+a2+a4的值；
（4）直接利用x=0时求出答案．
解答 解：（1）∵（2x-1）5=a5x5+a4x4+a3x3+a2x2+a1x+a0，
∴当x=1时，1=a0+a1+a2+a3+a4+a5①；
（2）令x=-1，得-a5+a4-a3+a2-a1+a0=-243②；
（3）由（2）（1）得：①+②，
2a4+2a2+2a0=-242，
即a0+a2+a4=-121；
（4）x=0，得=a0-1．
点评 此题主要考查了代数式求值，解题的关键是给x一些特殊值，然后再联立解答．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
17．下列调查适合作抽样调查的是（ ）
| A． | 了解江苏教育节目“服务到家”栏目的收视率 | |
| B． | 了解某甲型H1N1确诊病人同机乘客的健康状况 | |
| C． | 了解某班每个学生家庭电脑的数量 | |
| D． | 企业在给职工做工作服前进行的尺寸大小的调查 |
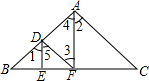如图所示，点D，A在直线AB上，点E，F在直线BC上，连接AC、DE、DF、AF．
如图，在?ABCD中，AD=12cm，AB=8cm，AE平分∠BAD交BC边于点E，则CE的长为4cm．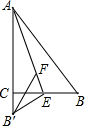
如图，在Rt△ABC，∠ACB=90°，现将Rt△ABC沿AE折叠，使AB边与AC边重合，B点落在B′处，在线段AE上取点F，使点F到AC，BC的距离相等，连接B′F，则∠B′FE的度数为（ ）
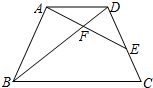如图，在梯形ABCD中，AD∥BC，AB=CD=8，AD=6，E在边CD上，AE与BD相交于点F，∠EAD=∠ABD．
已知：如图，在?ABCD中，点E、F在AC上，且AE=CF．求证：四边形EBFD是平行四边形．