题目内容
11.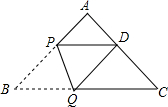 如图,在三角形ABC中,∠A=90°,AB=AC=2,将△ABC折叠,使点B落在边AC上点D (不与点A重合)处,折痕为PQ,当重叠部分△PQD为等腰三角形时,则AD的长为2或2$\sqrt{2}$-2.
如图,在三角形ABC中,∠A=90°,AB=AC=2,将△ABC折叠,使点B落在边AC上点D (不与点A重合)处,折痕为PQ,当重叠部分△PQD为等腰三角形时,则AD的长为2或2$\sqrt{2}$-2.
分析 根据等腰三角形的定义,分①PD=DQ时,BP=BQ,再根据翻折变换前后的线段相等判断出BP=BQ=PD=DQ,从而得到四边形BQDP是菱形,根据菱形的对边平行可得PD∥BC,BP∥DQ,然后判断出△APD和△CDQ都是等腰直角三角形,根据等腰直角三角形的性质用AD表示出PD、CD,然后根据AC的长度列方程求解即可;②DQ=PQ时,BQ=PQ,求出△BPQ是等腰直角三角形,点B与点C重合,从而得到AD=AC;③PD=PQ时,PQ=BP,然后求出△BPQ是等腰直角三角形,点B与点A重合,不符合题意.
解答 解:①PD=DQ时,BP=BQ,
由翻折变换得,BP=PD,BQ=DQ,
所以,BP=BQ=PD=DQ,
所以,四边形BQDP是菱形,
所以,PD∥BC,BP∥DQ,
∵∠A=90°,AB=AC,
∴△ABC是等腰直角三角形,
∴△APD和△CDQ都是等腰直角三角形,
在Rt△APD中,PD=$\sqrt{2}$AD,
在Rt△CDQ中,CD=DQ,
∵PD=DQ,
∴CD=$\sqrt{2}$AD,
∵AC=AD+CD,
∴AD+$\sqrt{2}$AD=2,
解得AD=2$\sqrt{2}$-2;
②DQ=PQ时,BQ=PQ,
所以,∠BPQ=∠B=45°,
所以,△BPQ是等腰直角三角形,
所以,点B与点C重合,
所以,AD=AC=2;
③PD=PQ时,PQ=BP,
所以,∠BQP=∠B=45°,
所以,△BPQ是等腰直角三角形,
所以,点B与点A重合,
此时,点B与点A重合,不符合题意,舍去;
综上所述,AD的长度为2或2$\sqrt{2}$-2.
故答案为:2或2$\sqrt{2}$-2.
点评 本题考查了翻折变换的性质,菱形的判定与性质,等腰直角三角形的判定与性质,等腰三角形的性质,综合题,难点在于分情况讨论.

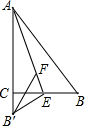 如图,在Rt△ABC,∠ACB=90°,现将Rt△ABC沿AE折叠,使AB边与AC边重合,B点落在B′处,在线段AE上取点F,使点F到AC,BC的距离相等,连接B′F,则∠B′FE的度数为( )
如图,在Rt△ABC,∠ACB=90°,现将Rt△ABC沿AE折叠,使AB边与AC边重合,B点落在B′处,在线段AE上取点F,使点F到AC,BC的距离相等,连接B′F,则∠B′FE的度数为( )| A. | 30° | B. | 36° | C. | 45° | D. | 60° |
| A. | a-1、a+1、$\sqrt{1+{a}^{2}}$ | B. | 3(a-1)、4(a-1)、5(a-1) | C. | a-1、a、a+1 | D. | a+2、a、$\sqrt{2{a}^{2}+4}$ |
| A. | a=1.5,b=2,c=3 | B. | a=3,b=4,c=5 | C. | a=6,b=8,c=10 | D. | a=7,b=24,c=25 |
| A. | $\root{3}{2}$ | B. | $\sqrt{-2}$ | C. | $\sqrt{(-2)^{2}}$ | D. | $\sqrt{a}$ |
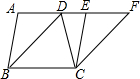 如图,在四边形ABCD中,AD∥BC,且AD<BC,连接BD,现将三角形ABD平移到三角形ECF的位置.
如图,在四边形ABCD中,AD∥BC,且AD<BC,连接BD,现将三角形ABD平移到三角形ECF的位置. 已知:如图,在?ABCD中,点E、F在AC上,且AE=CF.求证:四边形EBFD是平行四边形.
已知:如图,在?ABCD中,点E、F在AC上,且AE=CF.求证:四边形EBFD是平行四边形.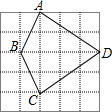 如图,5×5网格的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,四边形ABCD的顶点A、B、C、D均在格点上,连接BD.
如图,5×5网格的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,四边形ABCD的顶点A、B、C、D均在格点上,连接BD.