题目内容
15. 如图所示,∠DAB=∠DCB=90°.CB=CD,且AD=3,AB=4,则AC的长为( )
如图所示,∠DAB=∠DCB=90°.CB=CD,且AD=3,AB=4,则AC的长为( )| A. | $\frac{7\sqrt{2}}{2}$ | B. | 5 | C. | $\frac{\sqrt{2}}{7}$ | D. | 7 |
分析 作CE⊥AB于E,作CF⊥AD于F,则四边形AECF是矩形,得出∠FCE=90°,证出∠DCF=∠BCE,由AAS证明△CDF≌△CBE,得出CF=CE,DF=BE,证出四边形AECF是正方形,得出AE=AF,设DF=BE=x,则AF=x+3,列出方程,解方程求出DF、AF,即可得出AC的长.
解答 解:作CE⊥AB于E,作CF⊥AD于F,如图所示: 则∠CFD=∠CEB=90°,四边形AECF是矩形,
则∠CFD=∠CEB=90°,四边形AECF是矩形,
∴∠FCE=90°,
∵∠DCB=90°,
∴∠DCF=∠BCE,
在△CDF和△CBE中,$\left\{\begin{array}{l}{∠CFD=∠CEB}&{\;}\\{∠DCF=∠BCE}&{\;}\\{CD=CB}&{\;}\end{array}\right.$,
∴△CDF≌△CBE(AAS),
∴CF=CE,DF=BE,
∴四边形AECF是正方形,
∴AE=AF,
设DF=BE=x,则AF=x+3,AE=4-x,
∴x+3=4-x,
解得:x=$\frac{1}{2}$,
∴DF=$\frac{1}{2}$,
∴AF=3+$\frac{1}{2}$=$\frac{7}{2}$,
∴AC=$\sqrt{2}$AF=$\frac{7\sqrt{2}}{2}$;
故选:A.
点评 本题考查了全等三角形的判定与性质、正方形的判定与性质、三角函数、矩形的判定;熟练掌握正方形的判定与性质,通过作辅助线构造三角形全等是解决问题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
5.下列运算正确的是( )
| A. | x3•x2=x6 | B. | (ab)2=ab2 | C. | (-m2)3=-m6 | D. | p6÷p3=2 |
3.下列说法正确的是( )
| A. | 81的算术平方根是9 | B. | 81的平方根是-9 | ||
| C. | -81的平方根是9 | D. | 49的算术平方根是±7 |
4. 如图,△ABC中,AB=BC,将△ABC绕点B顺时针旋转到△A1BC1,使得A1C1∥AB,A1B交AC于点E,A1C1分别交AC、BC于点D、F,则∠EBF的取值范围是( )
如图,△ABC中,AB=BC,将△ABC绕点B顺时针旋转到△A1BC1,使得A1C1∥AB,A1B交AC于点E,A1C1分别交AC、BC于点D、F,则∠EBF的取值范围是( )
 如图,△ABC中,AB=BC,将△ABC绕点B顺时针旋转到△A1BC1,使得A1C1∥AB,A1B交AC于点E,A1C1分别交AC、BC于点D、F,则∠EBF的取值范围是( )
如图,△ABC中,AB=BC,将△ABC绕点B顺时针旋转到△A1BC1,使得A1C1∥AB,A1B交AC于点E,A1C1分别交AC、BC于点D、F,则∠EBF的取值范围是( )| A. | 0°~180° | B. | 0~90° | C. | 0°~60° | D. | 30°~180° |
 已知,如图在四边形ABCD中,AB=CD,则添加一个AD=BC条件(只需填写一种)可以使得四边形ABCD为平行四边形.
已知,如图在四边形ABCD中,AB=CD,则添加一个AD=BC条件(只需填写一种)可以使得四边形ABCD为平行四边形.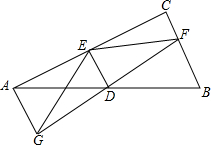 已知:如图,△ABC中,∠C=90°,D为AB的中点,E、F分别在AC、BC上,且DE⊥DF.延长FD到G,使DG=DF,连结GE,GA.
已知:如图,△ABC中,∠C=90°,D为AB的中点,E、F分别在AC、BC上,且DE⊥DF.延长FD到G,使DG=DF,连结GE,GA. 台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力,据气象观测,距沿海某城市A的正南方向220km的B处有一台风中心,其中心最大风力为12级,每远离台风中心20km,风力就会减弱一级,该台风中心现在正以15km/h的速度沿北偏东30°的方向移动,且台风中心风力不变,如图,若城市所受的风力达到或超过4级,则称为受台风影响.
台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力,据气象观测,距沿海某城市A的正南方向220km的B处有一台风中心,其中心最大风力为12级,每远离台风中心20km,风力就会减弱一级,该台风中心现在正以15km/h的速度沿北偏东30°的方向移动,且台风中心风力不变,如图,若城市所受的风力达到或超过4级,则称为受台风影响. 如图,AB∥DE,点F、C在AD上,AB=DE,且AF=FC=CD.
如图,AB∥DE,点F、C在AD上,AB=DE,且AF=FC=CD.