题目内容
20. 台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力,据气象观测,距沿海某城市A的正南方向220km的B处有一台风中心,其中心最大风力为12级,每远离台风中心20km,风力就会减弱一级,该台风中心现在正以15km/h的速度沿北偏东30°的方向移动,且台风中心风力不变,如图,若城市所受的风力达到或超过4级,则称为受台风影响.
台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力,据气象观测,距沿海某城市A的正南方向220km的B处有一台风中心,其中心最大风力为12级,每远离台风中心20km,风力就会减弱一级,该台风中心现在正以15km/h的速度沿北偏东30°的方向移动,且台风中心风力不变,如图,若城市所受的风力达到或超过4级,则称为受台风影响.(1)该城市是否受到这次台风的影响?请说明理由;
(2)若会受台风影响,那么台风影响该城市的持续时间有多长?该城市受到台风影响的最大风力为几级?
分析 (1)求是否会受到台风的影响,其实就是求A到BC的距离是否大于台风影响范围的半径,如果大于,则不受影响,反之则受影响.如果过A作AD⊥BC于D,AD就是所求的线段.直角三角形ABD中,有∠ABD的度数,有AB的长,AD就不难求出了.
(2)受台风影响时,台风中心移动的距离,应该是A为圆心,台风影响范围的半径为半径,所得圆截得的BC上的线段的长即EF得长,可通过在直角三角形AED和AFD中,根据勾股定理求得.有了路程,有了速度,时间就可以求出了,风力最大时,台风中心应该位于D点,然后根据题目给出的条件判断出时几级风.
解答  解:(1)该城市会受到这次台风的影响.
解:(1)该城市会受到这次台风的影响.
理由是:如图,过A作AD⊥BC于D.在Rt△ABD中,
∵∠ABD=30°,AB=220,
∴AD=$\frac{1}{2}$AB=110,
∵城市受到的风力达到或超过四级,则称受台风影响,
∴受台风影响范围的半径为20×(12-4)=160.
∵110<160,
∴该城市会受到这次台风的影响;
(2)如图以A为圆心,160为半径作⊙A交BC于E、F.
则AE=AF=160.
∴台风影响该市持续的路程为:EF=2DE=2$\sqrt{16{0}^{2}-11{0}^{2}}$=60$\sqrt{15}$.
∴台风影响该市的持续时间t=60$\sqrt{15}$÷15=4$\sqrt{15}$(小时),
∵AD距台风中心最近,
∴该城市受到这次台风最大风力为:12-(110÷20)=6.5(级).
点评 本题考查了勾股定理的应用,解题的关键是将实际问题转化为直角三角形中的数学问题,可通过作辅助线构造直角三角形,再把条件和问题转化到直角三角形中,使问题解决.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
10.已知a=-(0.2)2,b=-22,c=(-$\frac{1}{2}$)-2,d=(-$\frac{1}{2}$)0,则比较a、b、c、d的大小结果是( )
| A. | a<b<c<d | B. | a<b<d<c | C. | b<a<d<c | D. | b<a<c<d |
15. 如图所示,∠DAB=∠DCB=90°.CB=CD,且AD=3,AB=4,则AC的长为( )
如图所示,∠DAB=∠DCB=90°.CB=CD,且AD=3,AB=4,则AC的长为( )
 如图所示,∠DAB=∠DCB=90°.CB=CD,且AD=3,AB=4,则AC的长为( )
如图所示,∠DAB=∠DCB=90°.CB=CD,且AD=3,AB=4,则AC的长为( )| A. | $\frac{7\sqrt{2}}{2}$ | B. | 5 | C. | $\frac{\sqrt{2}}{7}$ | D. | 7 |
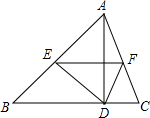 如图,在△ABC中,AD是高,将△ABC折叠,使点A和的D重合,折痕为EF,若AB=7cm,BC=6cm,AC=5cm,则△DEF的周长是9cm.
如图,在△ABC中,AD是高,将△ABC折叠,使点A和的D重合,折痕为EF,若AB=7cm,BC=6cm,AC=5cm,则△DEF的周长是9cm. 在平面直角坐标系xOy中,矩形OABC如图放置,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2次碰到矩形的边时,点P的坐标为(7,4);当点P第6次碰到矩形的边时,点P的坐标为(0,3);当点P第2015次碰到矩形的边时,点P的坐标为(1,4).
在平面直角坐标系xOy中,矩形OABC如图放置,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2次碰到矩形的边时,点P的坐标为(7,4);当点P第6次碰到矩形的边时,点P的坐标为(0,3);当点P第2015次碰到矩形的边时,点P的坐标为(1,4).