Question

10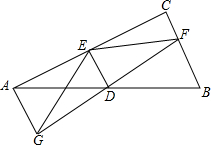．已知：如图，△ABC中，∠C=90°，D为AB的中点，E、F分别在AC、BC上，且DE⊥DF．延长FD到G，使DG=DF，连结GE，GA．
求证：
（1）GE=FE
（2）∠EAG=90°
（3）AE²+BF²=EF²．

Answer 1

分析 （1）由DE⊥DF，DG=DF，根据线段垂直平分线上的点到线段两端的距离相等即可证明GE=FE；
（2）先利用SAS证明△ADG≌△BDF，根据全等三角形的性质得出AG=BF，∠GAD=∠FBD，由内错角相等两直线平行得出AG∥BC，再根据两直线平行同旁内角互补得到∠EAG=180°-∠C=90°；
（3）在Rt△AEG中利用勾股定理得出AE²+AG²=EG²，又AG=BF，EG=EF，等量代换即可证明AE²+BF²=EF²．

解答 证明：（1）∵DE⊥DF，DG=DF，
∴GE=FE；

（2）在△ADG与△BDF中，
$\left\{\begin{array}{l}{AD=BD}\\{∠ADG=∠BDG}\\{DG=DF}\end{array}\right.$，
∴△ADG≌△BDF（SAS），
∴AG=BF，∠GAD=∠FBD，
∴AG∥BC，
∴∠EAG=180°-∠C=90°；

（3）在Rt△AEG中，∵∠EAG=90°，
∴AE²+AG²=EG²，
∵AG=BF，EG=EF，
∴AE²+BF²=EF²．

点评 本题考查了全等三角形的判定与性质，线段垂直平分线的性质，平行线的判定与性质，勾股定理，难度适中．证明△ADG≌△BDF是解题的关键．