题目内容
已知A(4,-2),B(a,b),C(0,2),且AB⊥x轴,△ABC的面积等于10,则点B的坐标为 .
考点:坐标与图形性质,三角形的面积
专题:计算题
分析:由于AB⊥x轴,则点A与点B的横坐标相同,AB的长为它们的纵坐标之差的绝对值,即a=4,AB=|b+2|,然后根据三角形面积公式得到
•4•|b+2|=10,再解方程求出b即可得到B点坐标.
| 1 |
| 2 |
解答:解:∵A(4,-2),B(a,b),AB⊥x轴,
∴a=4,AB=|b+2|,
∵△ABC的面积等于10,
∴
•4•|b+2|=10,解得b=3或b=-7,
∴点B的坐标为(4,3)或(4,-7).
故答案为(4,3)或(4,-7).
∴a=4,AB=|b+2|,
∵△ABC的面积等于10,
∴
| 1 |
| 2 |
∴点B的坐标为(4,3)或(4,-7).
故答案为(4,3)或(4,-7).
点评:本题考查了坐标与图形性质:利用点的坐标计算相应的线段长和判断线段与坐标轴的关系.记住三角形面积公式.

练习册系列答案
相关题目
函数y=2-
的最值是( )
| -x2+4x |
| A、y最小值=-2,y最大值=2 | ||||
| B、y最小值=1,y最大值=2 | ||||
| C、y最小值=0,y最大值=2 | ||||
D、y最小值=-
|
 如图,△ABC中,AB=AC,D是BC边的中点,CE⊥AB于E.试说明:△ABD∽CBE.
如图,△ABC中,AB=AC,D是BC边的中点,CE⊥AB于E.试说明:△ABD∽CBE.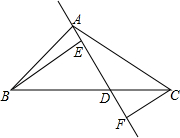 在△ABC中,AD是过A的一条射线,交BC于D,过B作BE⊥AD于E,过C作CF⊥AD于F.
在△ABC中,AD是过A的一条射线,交BC于D,过B作BE⊥AD于E,过C作CF⊥AD于F.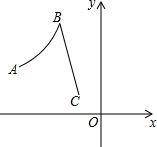 如图,已知A点坐标为(-6,3),C点坐标为(-2,1),曲线段AB是反比例函数图象的一部分,线段BC是一次函数图象的一部分,若B点到x轴的距离等于到y轴距离的2倍.
如图,已知A点坐标为(-6,3),C点坐标为(-2,1),曲线段AB是反比例函数图象的一部分,线段BC是一次函数图象的一部分,若B点到x轴的距离等于到y轴距离的2倍.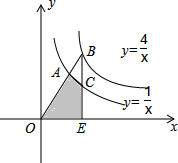 如图,过原点的直线交双曲线y=
如图,过原点的直线交双曲线y=