题目内容
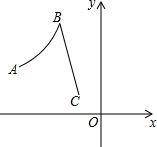 如图,已知A点坐标为(-6,3),C点坐标为(-2,1),曲线段AB是反比例函数图象的一部分,线段BC是一次函数图象的一部分,若B点到x轴的距离等于到y轴距离的2倍.
如图,已知A点坐标为(-6,3),C点坐标为(-2,1),曲线段AB是反比例函数图象的一部分,线段BC是一次函数图象的一部分,若B点到x轴的距离等于到y轴距离的2倍.(1)求B点坐标,并求线段BC所在直线的解析式;
(2)点P(m,t)在曲线段AB上,点Q(n,t)在线段BC上,且点P与点Q不重合,求n的取值范围.
考点:反比例函数综合题
专题:
分析:(1)首先利用待定系数法求得反比例函数的解析式,B点到x轴的距离等于到y轴距离的2倍.则设B的横坐标是m(m<0),则纵坐标是-2m,把(m,-2m)代入反比例函数的解析式即可求得m的值,即B的坐标,然后利用待定系数法求得直线BC的解析式;
(2)点P和Q与x轴平行,求得当P在A点时n的值,即可求得n的范围.
(2)点P和Q与x轴平行,求得当P在A点时n的值,即可求得n的范围.
解答:解:(1)设反比例函数的解析式是y=
,把(-6,3)代入得:k=-18,
则反比例函数的解析式是y=-
.
设B的横坐标是m(m<0),则纵坐标是-2m,把(m,-2m)代入y=-
得:-2m2=-18,
解得:m=-3或m=3(舍去),
则B的坐标是(-3,6).
设直线BC的解析式是y=nx+b,则
,
解得:
,
则直线BC的解析式是:y=-5x+11;
(2)在y=-5x+11中,令y=3,则-5x+11=3,解得:x=
.
则n的范围是:-3<n≤
.
| k |
| x |
则反比例函数的解析式是y=-
| 18 |
| x |
设B的横坐标是m(m<0),则纵坐标是-2m,把(m,-2m)代入y=-
| 18 |
| x |
解得:m=-3或m=3(舍去),
则B的坐标是(-3,6).
设直线BC的解析式是y=nx+b,则
|
解得:
|
则直线BC的解析式是:y=-5x+11;
(2)在y=-5x+11中,令y=3,则-5x+11=3,解得:x=
| 8 |
| 5 |
则n的范围是:-3<n≤
| 8 |
| 5 |
点评:本题考查了待定系数法求函数的解析式,正确求得B的坐标是解决本题的关键.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
 如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,羊圈的边长AB为多少米?
如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,羊圈的边长AB为多少米? 如图,在□ABCD和□CEFG中,AD=6,CE=2
如图,在□ABCD和□CEFG中,AD=6,CE=2