题目内容
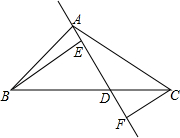 在△ABC中,AD是过A的一条射线,交BC于D,过B作BE⊥AD于E,过C作CF⊥AD于F.
在△ABC中,AD是过A的一条射线,交BC于D,过B作BE⊥AD于E,过C作CF⊥AD于F.(1)若M是BC中点.求证:FM=EM;
(2)若∠BAC=90°,AB=AC,线段BE、CF、EF之间存在确定的数量关系吗?试证明你的结论;
(3)当AD在△ABC的外部时,在(1)的条件下,(1)中的结论还存在吗?
(4)当AD在△ABC的外部时,在(2)的条件下,(2)中的结论还存在吗?试证明你的猜想.
考点:全等三角形的判定与性质
专题:
分析:(1)连接EM,延长CF与EM交于N,易证∠EBM=∠NCM,即可证明△BME≌△CNM,可得ME=MN,再根据直角三角形斜边中线等于斜边一半的性质可得MF=
NE,即可解题;
(2)易证∠ABE=∠CAF,即可证明△BAE≌△CAF,可得AF=BE,AE=CF,根据AF=AE+EF即可解题;
(3)连接EM,延长CF与EM交于N,易证∠EBM=∠NCM,即可证明△BME≌△CNM,可得ME=MN,再根据直角三角形斜边中线等于斜边一半的性质可得MF=
NE,即可解题;
(4)易证∠ABE=∠CAF,即可证明△BAE≌△CAF,可得AF=BE,AE=CF,根据EF=AE+AF即可解题.
| 1 |
| 2 |
(2)易证∠ABE=∠CAF,即可证明△BAE≌△CAF,可得AF=BE,AE=CF,根据AF=AE+EF即可解题;
(3)连接EM,延长CF与EM交于N,易证∠EBM=∠NCM,即可证明△BME≌△CNM,可得ME=MN,再根据直角三角形斜边中线等于斜边一半的性质可得MF=
| 1 |
| 2 |
(4)易证∠ABE=∠CAF,即可证明△BAE≌△CAF,可得AF=BE,AE=CF,根据EF=AE+AF即可解题.
解答:证明:(1)连接EM,延长CF与EM交于N,

∵BE⊥AD,CF⊥AD,
∴BE∥CF,
∴∠EBM=∠NCM,
∵在△BME和△CNM中,
,
∴△BME≌△CNM,(ASA)
∴ME=MN,
∵RT△EFN中,MF=
NE,
∴MF=ME;
(2)BE=CF+EF,
理由:∵∠BAE+∠CAF=90°,∠BAE+ABE=90°,
∴∠ABE=∠CAF,
∵在△BAE和△CAF中,
,
∴△BAE≌△CAF,(AAS)
∴AF=BE,AE=CF,
∵AF=AE+EF,
∴BE=CF+EF;
(3)还存在,
理由:如图,连接EM,延长CF与EM交于N,

∵BE⊥AD,CF⊥AD,
∴BE∥CF,
∴∠EBM=∠NCM,
∵在△BME和△CNM中,
,
∴△BME≌△CNM,(ASA)
∴ME=MN,
∵RT△EFN中,MF=
NE,
∴MF=ME;
(4)不存在,新结论为BE+CF=EF.
理由:如图,

∵∠BAE+∠CAF=90°,∠BAE+ABE=90°,
∴∠ABE=∠CAF,
∵在△BAE和△CAF中,
,
∴△BAE≌△CAF,(AAS)
∴AF=BE,AE=CF,
∵EF=AE+AF,
∴EF=CF+BE.

∵BE⊥AD,CF⊥AD,
∴BE∥CF,
∴∠EBM=∠NCM,
∵在△BME和△CNM中,
|
∴△BME≌△CNM,(ASA)
∴ME=MN,
∵RT△EFN中,MF=
| 1 |
| 2 |
∴MF=ME;
(2)BE=CF+EF,
理由:∵∠BAE+∠CAF=90°,∠BAE+ABE=90°,
∴∠ABE=∠CAF,
∵在△BAE和△CAF中,
|
∴△BAE≌△CAF,(AAS)
∴AF=BE,AE=CF,
∵AF=AE+EF,
∴BE=CF+EF;
(3)还存在,
理由:如图,连接EM,延长CF与EM交于N,

∵BE⊥AD,CF⊥AD,
∴BE∥CF,
∴∠EBM=∠NCM,
∵在△BME和△CNM中,
|
∴△BME≌△CNM,(ASA)
∴ME=MN,
∵RT△EFN中,MF=
| 1 |
| 2 |
∴MF=ME;
(4)不存在,新结论为BE+CF=EF.
理由:如图,

∵∠BAE+∠CAF=90°,∠BAE+ABE=90°,
∴∠ABE=∠CAF,
∵在△BAE和△CAF中,
|
∴△BAE≌△CAF,(AAS)
∴AF=BE,AE=CF,
∵EF=AE+AF,
∴EF=CF+BE.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△BME≌△CNM和△BAE≌△CAF是解题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,羊圈的边长AB为多少米?
如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,羊圈的边长AB为多少米? 如图,已知∠AOC=90°,OP平分∠AOB,OQ平分∠BOC,求∠POQ的度数.
如图,已知∠AOC=90°,OP平分∠AOB,OQ平分∠BOC,求∠POQ的度数.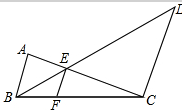 如图,AB∥EF∥CD,已知AB=20,CD=80,求EF的长.
如图,AB∥EF∥CD,已知AB=20,CD=80,求EF的长. 如图所示,已知A、B、C、D,请在图中找出一点P,使PA+PB+PC+PD最小.
如图所示,已知A、B、C、D,请在图中找出一点P,使PA+PB+PC+PD最小.