题目内容
函数y=2-
的最值是( )
| -x2+4x |
| A、y最小值=-2,y最大值=2 | ||||
| B、y最小值=1,y最大值=2 | ||||
| C、y最小值=0,y最大值=2 | ||||
D、y最小值=-
|
考点:二次函数的最值
专题:
分析:把被开方数配方,然后根据平方数非负数的性质和二次函数的最值问题解答即可.
解答:解:∵y=2-
=2-
,
∴当x=2时,y最小=2-2=0,
当x=0或4时,y最大=2-0=2.
故选C.
| -x2+4x |
| -(x-2)2+4 |
∴当x=2时,y最小=2-2=0,
当x=0或4时,y最大=2-0=2.
故选C.
点评:本题考查了二次函数的最值问题,主要利用了配方法和平方数非负数的性质.

练习册系列答案
相关题目
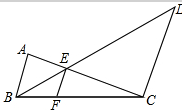 如图,AB∥EF∥CD,已知AB=20,CD=80,求EF的长.
如图,AB∥EF∥CD,已知AB=20,CD=80,求EF的长. 如图所示,已知A、B、C、D,请在图中找出一点P,使PA+PB+PC+PD最小.
如图所示,已知A、B、C、D,请在图中找出一点P,使PA+PB+PC+PD最小.