题目内容
12.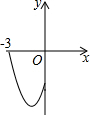 在平面直角坐标系中,二次函数y=x2+2x-3(-3≤x≤0)的图象如图所示,点A(x1,y1),B(x2,y2)(x1<x2)是该二次函数图象上的两点,则下列结论中错误的是②④(填序号)
在平面直角坐标系中,二次函数y=x2+2x-3(-3≤x≤0)的图象如图所示,点A(x1,y1),B(x2,y2)(x1<x2)是该二次函数图象上的两点,则下列结论中错误的是②④(填序号)①y1<y2;②y的最小值是-4;③y1>y2;④y的最大值为0.
分析 先根据题意得出抛物线的顶点坐标,再由二次函数的性质对各选项进行逐一判断即可.
解答 解:∵二次函数的解析式为:y=x2+2x-3(-3≤x≤0),
∴其顶点坐标为(-1,-4).
∵点A(x1,y1),B(x2,y2)的位置不确定,
∴y1与y2的大小不确定,故①③错误;
∵抛物线开口向上,顶点坐标为(-1,-4),
∴y的最小值是-4,故②正确;
∵-3≤x≤0,
∴y的最大值为0,故④正确.
故答案为:②④.
点评 本题考查的是二次函数图象上点的坐标特点,熟知二次函数图象上点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
3.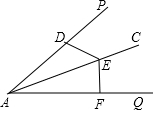 如图,已知AC平分∠PAQ,D、E、F分别是AP、AC、AQ上的三个动点,下列说法不正确的是( )
如图,已知AC平分∠PAQ,D、E、F分别是AP、AC、AQ上的三个动点,下列说法不正确的是( )
 如图,已知AC平分∠PAQ,D、E、F分别是AP、AC、AQ上的三个动点,下列说法不正确的是( )
如图,已知AC平分∠PAQ,D、E、F分别是AP、AC、AQ上的三个动点,下列说法不正确的是( )| A. | DE⊥AP,EF⊥AQ,可推出AD=AF | B. | 若DE=EF,可推出AD=AF | ||
| C. | 若∠DEA=∠FEA,可推出AD=AF | D. | 若∠ADE=∠AFE,可推出AD=AF |
7.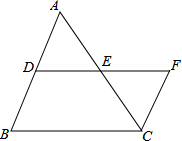 如图,D、E是△ABC的边AB、AC的中点,延长DE至F使EF=DE,则S△CFE:S四边形BCFD的值为( )
如图,D、E是△ABC的边AB、AC的中点,延长DE至F使EF=DE,则S△CFE:S四边形BCFD的值为( )
 如图,D、E是△ABC的边AB、AC的中点,延长DE至F使EF=DE,则S△CFE:S四边形BCFD的值为( )
如图,D、E是△ABC的边AB、AC的中点,延长DE至F使EF=DE,则S△CFE:S四边形BCFD的值为( )| A. | 1:3 | B. | 2:3 | C. | 1:4 | D. | 2:5 |
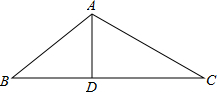 如图,D为△ABC的BC边上的一点,AB=10,AD=6,DC=2AD,BD=$\frac{2}{3}$DC.
如图,D为△ABC的BC边上的一点,AB=10,AD=6,DC=2AD,BD=$\frac{2}{3}$DC.
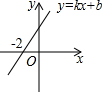 如图,一次函数y=kx+b的图象与x轴的交点坐标为(-2,0),则下列说法:
如图,一次函数y=kx+b的图象与x轴的交点坐标为(-2,0),则下列说法: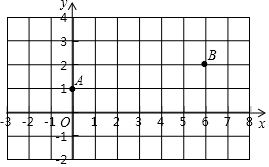 如图,在平面直角坐标系xOy中,已知点A(0,1),B(6,2),在x轴上找一点P,使得PA+PB最小,则点P的坐标是(4,0),此时△PAB的面积是2.
如图,在平面直角坐标系xOy中,已知点A(0,1),B(6,2),在x轴上找一点P,使得PA+PB最小,则点P的坐标是(4,0),此时△PAB的面积是2. 如图,⊙O的内接△ABC中,已知BC=3,∠A=60°,求⊙O的半径长.
如图,⊙O的内接△ABC中,已知BC=3,∠A=60°,求⊙O的半径长.