题目内容
17.如图,抛物线y=ax2+bx+c(a>0)的顶点为M,直线y=m与x轴平行,且与抛物线交于点A,B,若△AMB为等腰直角三角形,我们把抛物线上A,B两点之间的部分与线段AB围成的图形称为该抛物线对应的准碟形,线段AB称为碟宽,顶点M称为碟顶,点M到线段AB的剧烈为碟高.(1)抛物线y=x2对应的碟宽为2;抛物线y=$\frac{1}{2}$x2对应的碟宽为4;抛物线y=ax2(a>0)对应的碟宽为$\frac{2}{a}$;抛物线y=a(x-3)2+2(a>0)对应的碟宽为$\frac{2}{a}$;
(2)利用图(1)中的结论:抛物线y=ax2-4ax-$\frac{5}{3}$(a>0)对应的碟宽为6,求抛物线的解析式.
(3)将抛物线yn=anx2+bnx+cn(an>0)的对应准蝶形记为Fn(n=1,2,3,…),定义F1,F2,…..Fn为相似准蝶形,相应的碟宽之比即为相似比.若Fn与Fn-1的相似比为$\frac{1}{2}$,且Fn的碟顶是Fn-1的碟宽的中点,现在将(2)中求得的抛物线记为y1,其对应的准蝶形记为F1.
①求抛物线y2的表达式;
②若F1的碟高为h1,F2的碟高为h2,…Fn的碟高为hn.则hn=$\frac{3}{{2}^{n-1}}$,Fn的碟宽右端点横坐标为3+$\frac{3}{{2}^{n-1}}$.

分析 (1)根据碟宽的定义以及等腰直角三角形的性质可以假设B(m,m),代入抛物线的解析式,求出A、B两点坐标即可解决问题.
(2)利用(1)中结论碟宽为$\frac{2}{a}$,列出方程即可解决问题.
(3)①由F2的碟宽:F1的碟宽=1:2,即$\frac{2}{{a}_{2}}$:$\frac{2}{{a}_{1}}$=1:2,由a1=$\frac{1}{3}$,可得a2=$\frac{2}{3}$,再求出y2的顶点坐标即可解决问题.
②先求出h1,h2,…,B1,B2,…的横坐标,探究规律后即可解决问题.
解答 解:(1)根据碟宽的定义以及等腰直角三角形的性质可以假设B(m,m).
①把B(m,m)代入y=x2,得到m=1或0(舍弃),
∴A(-1,1),B(1,1),
∴AB=2,即碟宽为2.
②把B(m,m)代入y=$\frac{1}{2}$x2,得到m=2或0(舍弃),
∴A(-2,2),B(2,2),
∴AB=4,即碟宽为4.
③把B(m,m)代入y=ax2,得到m=$\frac{1}{a}$或0(舍弃),
∴A(-$\frac{1}{a}$,$\frac{1}{a}$),B($\frac{1}{a}$,$\frac{1}{a}$),
∴AB=$\frac{2}{a}$,即碟宽为$\frac{2}{a}$.
④根据碟宽的定义以及等腰直角三角形的性质,碟宽的大小与顶点的位置无关,所以$\frac{2}{a}$.
故答案分别为2,4,$\frac{2}{a}$,$\frac{2}{a}$.
(2)由(1)可知碟宽为$\frac{2}{a}$=6,
∴a=$\frac{1}{3}$,
∴抛物线的解析式为y=$\frac{1}{3}$x2-$\frac{4}{3}$x-$\frac{5}{3}$.
(3)①∵y1=$\frac{1}{3}$x2-$\frac{4}{3}$x-$\frac{5}{3}$=$\frac{1}{3}$(x-2)2-3的碟宽AB在x轴上,(A在B左边),
∴A(-1,0),B(5,0),
∴抛物线y2的顶点坐标为(2,0),
∵F2的碟宽:F1的碟宽=1:2,
∴$\frac{2}{{a}_{2}}$:$\frac{2}{{a}_{1}}$=1:2,
∵a1=$\frac{1}{3}$,
∴a2=$\frac{2}{3}$,
∴抛物线y2的解析式为y=$\frac{2}{3}$(x-2)2.
②∵hn:hn-1=1:2,h1=3,
∴h2=$\frac{3}{2}$,h3=$\frac{3}{{2}^{2}}$,h4=$\frac{3}{{2}^{3}}$,…,hn=$\frac{3}{{2}^{n-1}}$,
点碟宽右端点B的 横坐标,B1的横坐标3,B2的横坐标为3+$\frac{3}{2}$,B3的横坐标为3+$\frac{3}{{2}^{2}}$,B4的横坐标为3+$\frac{3}{{2}^{3}}$,…Bn的横坐标为3+$\frac{3}{{2}^{n-1}}$,
故答案为$\frac{3}{{2}^{n-1}}$,3+$\frac{3}{{2}^{n-1}}$.
点评 本题考查二次函数综合题,等腰直角三角形的性质、“准碟形”的定义等知识,解题的关键是理解题意,灵活运用所学知识解决问题,学会从特殊到一般的探究规律的方法,属于中考压轴题.

 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案| 与标准质量的差值(克) | -5 | -2 | 0 | 1 | 3 | 6 |
| 袋数(袋) | 1 | 4 | 3 | 4 | 5 | 3 |
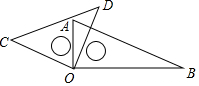 如图,小明将自己用的一副三角板摆成如图形状,下列结论错误的是( )
如图,小明将自己用的一副三角板摆成如图形状,下列结论错误的是( )| A. | ∠COA=∠DOB | B. | ∠AOD=∠B | C. | ∠COA与∠DOA互余 | D. | ∠AOD与∠COB互补 |
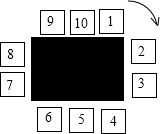 如图,在一个桌子周围放置着10个箱子,按顺时针方向编为1~10号.小华在1号箱子中投入一颗红球后,沿着桌子按顺时针方向行走,每经过一个箱子就根据下列规则投入一颗球:
如图,在一个桌子周围放置着10个箱子,按顺时针方向编为1~10号.小华在1号箱子中投入一颗红球后,沿着桌子按顺时针方向行走,每经过一个箱子就根据下列规则投入一颗球: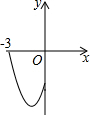 在平面直角坐标系中,二次函数y=x2+2x-3(-3≤x≤0)的图象如图所示,点A(x1,y1),B(x2,y2)(x1<x2)是该二次函数图象上的两点,则下列结论中错误的是②④(填序号)
在平面直角坐标系中,二次函数y=x2+2x-3(-3≤x≤0)的图象如图所示,点A(x1,y1),B(x2,y2)(x1<x2)是该二次函数图象上的两点,则下列结论中错误的是②④(填序号)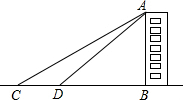 某班开展测量教学楼高度的综合实践活动.大家完成任务的方法有很多种,其中一种方法是:如图,他们在C点测得教学楼AB的顶部点A的仰角为30°,然后向教学楼前进20米到达点D,在点D测得点A的仰角为60°,且B,C,D三点在一条直线上.请你根据这些数据,求出这幢教学楼AB的高度.
某班开展测量教学楼高度的综合实践活动.大家完成任务的方法有很多种,其中一种方法是:如图,他们在C点测得教学楼AB的顶部点A的仰角为30°,然后向教学楼前进20米到达点D,在点D测得点A的仰角为60°,且B,C,D三点在一条直线上.请你根据这些数据,求出这幢教学楼AB的高度.