题目内容
1．
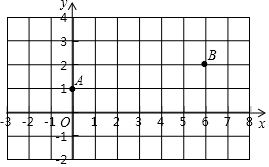如图，在平面直角坐标系xOy中，已知点A（0，1），B（6，2），在x轴上找一点P，使得PA+PB最小，则点P的坐标是（4，0），此时△PAB的面积是2．
分析 作点A关于x轴的对称点A′，连结A′B交x轴与点P，从而可得到点P的坐标，然后依据三角形的面积公式求解即可．
解答 解：作点A关于x轴的对称点A′，连结A′B交x轴与点P．
点P的坐标为（4，0），S△PAB=$\frac{1}{2}$×4×1=2．
故答案为：（4，0）；2．
点评 本题主要考查的是轴对称--最短路径问题，依据题意画出图形是解题的关键．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
如图，在四边形ABCD中，AB=8，BC=6，∠B=90°，AD=CD=5$\sqrt{2}$，求四边形ABCD的面积．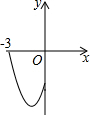
在平面直角坐标系中，二次函数y=x2+2x-3（-3≤x≤0）的图象如图所示，点A（x1，y1），B（x2，y2）（x1＜x2）是该二次函数图象上的两点，则下列结论中错误的是②④（填序号）
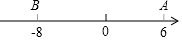已知数轴上两点A、B对应的数分别是6，-8，M、N为数轴上两个动点，点M从A点出发向左运动，速度为每秒2个单位长度，与此同时，点N从B点出发向右运动，速度为M点的3倍，经过多长时间，点M与点N相距50个单位长度？这时点M、N所对应的数分别是多少？
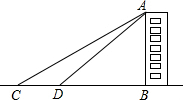某班开展测量教学楼高度的综合实践活动．大家完成任务的方法有很多种，其中一种方法是：如图，他们在C点测得教学楼AB的顶部点A的仰角为30°，然后向教学楼前进20米到达点D，在点D测得点A的仰角为60°，且B，C，D三点在一条直线上．请你根据这些数据，求出这幢教学楼AB的高度．
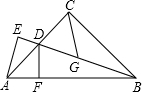已知：如图，在△ABC中，∠ACB=90°，AC=BC，BD平分∠ABC，BD交AC于点D，过点D作DF⊥AB于点F，过点A作BD的垂线，交BD的延长线于点E，点G是BD的中点．
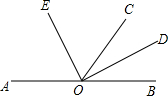如图，O是直线AB上的一点，OC为任意一条射线，OD平分∠BOC，OE平分∠AOC．
11．把弯曲的公路改直，能够缩短行程，这样的道理是（ ）
| A． | 两点确定一条直线 | B． | 两点确定一条线段 | ||
| C． | 两点之间线段最短 | D． | 两点之间直线最短 |