题目内容
2. 如图,⊙O的内接△ABC中,已知BC=3,∠A=60°,求⊙O的半径长.
如图,⊙O的内接△ABC中,已知BC=3,∠A=60°,求⊙O的半径长.
分析 作直径BD,连接CD,根据圆周角定理得到∠BCD=90°,设CD=x,根据勾股定理列出方程,解方程即可.
解答 解:作直径BD,连接CD,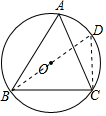
则∠BCD=90°,
∠D=∠A=60°,
∴∠DBC=30°,
设CD=x,则BD=2x,
由勾股定理得(2x)2=32+x2,
解得x=$\sqrt{3}$,
∴OB=$\frac{1}{2}$BD=x=$\sqrt{3}$,
⊙O的半径长$\sqrt{3}$.
点评 本题考查的是三角形的外接圆和外心的概念和性质,掌握圆周角定理、相似三角形的判定和性质是解题的关键.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
17.两个角,它们的比是7:3,差为36°,则这两个角的关系是( )
| A. | 互余 | B. | 互补 | ||
| C. | 既不互余也不互补 | D. | 不确定 |
7.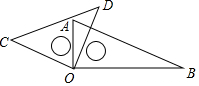 如图,小明将自己用的一副三角板摆成如图形状,下列结论错误的是( )
如图,小明将自己用的一副三角板摆成如图形状,下列结论错误的是( )
 如图,小明将自己用的一副三角板摆成如图形状,下列结论错误的是( )
如图,小明将自己用的一副三角板摆成如图形状,下列结论错误的是( )| A. | ∠COA=∠DOB | B. | ∠AOD=∠B | C. | ∠COA与∠DOA互余 | D. | ∠AOD与∠COB互补 |
11.把弯曲的公路改直,能够缩短行程,这样的道理是( )
| A. | 两点确定一条直线 | B. | 两点确定一条线段 | ||
| C. | 两点之间线段最短 | D. | 两点之间直线最短 |
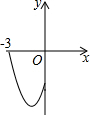 在平面直角坐标系中,二次函数y=x2+2x-3(-3≤x≤0)的图象如图所示,点A(x1,y1),B(x2,y2)(x1<x2)是该二次函数图象上的两点,则下列结论中错误的是②④(填序号)
在平面直角坐标系中,二次函数y=x2+2x-3(-3≤x≤0)的图象如图所示,点A(x1,y1),B(x2,y2)(x1<x2)是该二次函数图象上的两点,则下列结论中错误的是②④(填序号)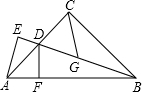 已知:如图,在△ABC中,∠ACB=90°,AC=BC,BD平分∠ABC,BD交AC于点D,过点D作DF⊥AB于点F,过点A作BD的垂线,交BD的延长线于点E,点G是BD的中点.
已知:如图,在△ABC中,∠ACB=90°,AC=BC,BD平分∠ABC,BD交AC于点D,过点D作DF⊥AB于点F,过点A作BD的垂线,交BD的延长线于点E,点G是BD的中点.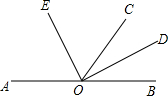 如图,O是直线AB上的一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.
如图,O是直线AB上的一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.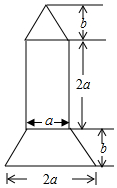 2016年9月15日晚,正值中秋佳节,我国“天宫二号”空间实验室顺利升空,这意味着中国载人航天工程将拥有首个真正意义的空间实验室.同学们倍受鼓舞,如图是某同学绘制的火箭模型截面图,上面是三角形,中间是长方形,下面是梯形,.
2016年9月15日晚,正值中秋佳节,我国“天宫二号”空间实验室顺利升空,这意味着中国载人航天工程将拥有首个真正意义的空间实验室.同学们倍受鼓舞,如图是某同学绘制的火箭模型截面图,上面是三角形,中间是长方形,下面是梯形,. 如图所示,小明和小亮用转盘做“配紫色”游戏(红色和蓝色在一起能配成紫色)小明转动的A盘被等分成4个扇形,小亮转动的B盘被等分成3个扇形,两人分别转动转盘一次.
如图所示,小明和小亮用转盘做“配紫色”游戏(红色和蓝色在一起能配成紫色)小明转动的A盘被等分成4个扇形,小亮转动的B盘被等分成3个扇形,两人分别转动转盘一次.