题目内容
2.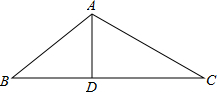 如图,D为△ABC的BC边上的一点,AB=10,AD=6,DC=2AD,BD=$\frac{2}{3}$DC.
如图,D为△ABC的BC边上的一点,AB=10,AD=6,DC=2AD,BD=$\frac{2}{3}$DC.(1)求BC的长;
(2)求△ABC的面积.
分析 (1)由DC=2AD,根据AD的长求出DC的长,进而求出BD的长即可;
(2)在直角三角形ABD中,由AB,AD以及BD的长,利用勾股定理的逆定理判断得到三角形为直角三角形,即可求出三角形ABC面积.
解答 解:(1)∵AD=6,DC=2AD,
∴DC=12,
∵BD=$\frac{2}{3}$DC,
∴BD=8,
BC=BD+DC=8+12=20;
(2)在△ABD中,AB=10,AD=6,BD=8,
∵AB2=AD2+BD2,
∴△ABD为直角三角形,即AD⊥BC,
∵BC=BD+DC=8+12=20,AD=6,
∴S△ABC=$\frac{1}{2}$×20×6=60.
点评 此题考查了勾股定理的逆定理,熟练掌握勾股定理的逆定理是解本题的关键.

练习册系列答案
相关题目
14.已知一个直角三角形的面积为84cm2,其中一条直角边的长为7cm,则该直角三角形的斜边的长为( )
| A. | 23cm | B. | 24cm | C. | 25cm | D. | 26cm |
 如图,AB为⊙O的直径,弦CD⊥弦AE,求证:$\widehat{BC}$=$\widehat{ED}$.
如图,AB为⊙O的直径,弦CD⊥弦AE,求证:$\widehat{BC}$=$\widehat{ED}$.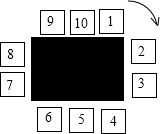 如图,在一个桌子周围放置着10个箱子,按顺时针方向编为1~10号.小华在1号箱子中投入一颗红球后,沿着桌子按顺时针方向行走,每经过一个箱子就根据下列规则投入一颗球:
如图,在一个桌子周围放置着10个箱子,按顺时针方向编为1~10号.小华在1号箱子中投入一颗红球后,沿着桌子按顺时针方向行走,每经过一个箱子就根据下列规则投入一颗球: 如图,在四边形ABCD中,AB=8,BC=6,∠B=90°,AD=CD=5$\sqrt{2}$,求四边形ABCD的面积.
如图,在四边形ABCD中,AB=8,BC=6,∠B=90°,AD=CD=5$\sqrt{2}$,求四边形ABCD的面积.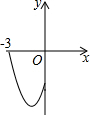 在平面直角坐标系中,二次函数y=x2+2x-3(-3≤x≤0)的图象如图所示,点A(x1,y1),B(x2,y2)(x1<x2)是该二次函数图象上的两点,则下列结论中错误的是②④(填序号)
在平面直角坐标系中,二次函数y=x2+2x-3(-3≤x≤0)的图象如图所示,点A(x1,y1),B(x2,y2)(x1<x2)是该二次函数图象上的两点,则下列结论中错误的是②④(填序号)