题目内容
14.已知A(1,m),B(n,1),直线l经过A、B两点,其解析式为y=-x+b.(1)当b=5时,求m、n的值;
(2)若此时双曲线y=$\frac{k}{x}$(x>0)也过A、B两点,求关于x的方程x2-bx+k=0的解.
分析 (1)把A(1,m),B(n,1)分别代入解析式即可求得;
(2)根据待定系数法求得k的值,确定方程为x2-5x+4=0,然后解方程即可.
解答 解:(1)当b=5时,y=-x+5,
把A(1,m)代入得:m=-1+5=4,
把B(n,1)代入得:1=-n+5,解得n=4,
即m=4,n=4;
(2)∵此时双曲线y=$\frac{k}{x}$(x>0)也过A、B两点,
∴k=1×4=4,
∴方程为x2-5x+4=0,
解得x1=4,x2=1.
点评 本题考查了反比例函数和一次函数的交点问题,待定系数法求反比例函数的解析式,一次函数图象上点的坐标特征以及方程的解等.

练习册系列答案
相关题目
9.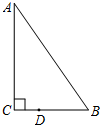 如图,△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m为( )
如图,△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m为( )
 如图,△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m为( )
如图,△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m为( )| A. | 70° | B. | 70°或120° | C. | 120° | D. | 80° |
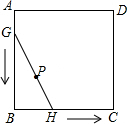 如图,正方形ABCD的边长为4,线段GH=AB,将GH的两端放在正方形的相邻的两边上同时滑动,如果G点从A点出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点H从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段GH的中点P所经过的路线围成的图形的面积为16-4π.
如图,正方形ABCD的边长为4,线段GH=AB,将GH的两端放在正方形的相邻的两边上同时滑动,如果G点从A点出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点H从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段GH的中点P所经过的路线围成的图形的面积为16-4π.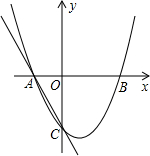 如图,抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(2,0)两点,与y轴交于点C(0,-2),过A、C画直线.
如图,抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(2,0)两点,与y轴交于点C(0,-2),过A、C画直线.