题目内容
5.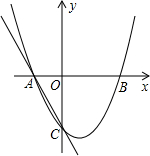 如图,抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(2,0)两点,与y轴交于点C(0,-2),过A、C画直线.
如图,抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(2,0)两点,与y轴交于点C(0,-2),过A、C画直线.(1)求二次函数的解析式;
(2)点P在x轴正半轴上,且PA=PC,求OP的长;
(3)若M为线段OB上的一个动点,过点M做MN平行于y轴交抛物线于点N,当点M运动到何处时,四边形ACNB的面积最大?求出此时点M的坐标及四边形ACNB面积的最大值?
分析 (1)先根据点的特点,设成交点式,用待定系数法求抛物线的解析式,
(2)设出点P的坐标,表示出PA=m+1,PC=$\sqrt{{m}^{2}+{2}^{2}}$,由PA=PC,求出m即可;
(3)把四边形分成△AOC,梯形OCNM,△BMN,分别求出面积,确定出函数解析式即可.
解答 解:(1)∵抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(2,0)两点,
∴设抛物线解析式为y=a(x+1)(x-2),
∴抛物线与y轴交于点C(0,-2),
∴-2=a×1×(-2),
∴a=1,
∴抛物线解析式为y=(x+1)(x-2)=x2-x-2,
(2)∵点P在x轴正半轴上,
∴设点P(m,0)(m>0),
∴PA=m+1,PC=$\sqrt{{m}^{2}+{2}^{2}}$,
∵PA=PC,
∴m+1=$\sqrt{{m}^{2}+{2}^{2}}$,
∴m=$\frac{3}{2}$,
∴OP=m=$\frac{3}{2}$;
(3)如图,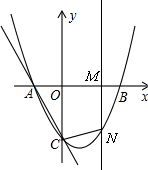
∵M为线段OB上的一个动点,
∴设M(n,0),(0<n<2)
∵过点M做MN平行于y轴交抛物线于点N,
∴n(n,n2-n-2)
∵OA=1,OC=2,OM=n,MN=|n2-n-2|=-(n2-n-2)=-n2+n+2,MB=2-n,
∴S四边形ACNB=S△AOC+S梯形OCNM+S△BMN
=$\frac{1}{2}$OA×OC+$\frac{1}{2}$(OC+MN)×OM+$\frac{1}{2}$MB×MN,
=$\frac{1}{2}$×1×2+$\frac{1}{2}$[2+(-n2+n+2)]n+$\frac{1}{2}$×(2-n)×(-n2+n+2)
=-n2+2n+3
=-(n-1)2+4,
∵0<n<2,
∴当n=1时,S四边形ACNB面积最大,最大值为4,
∴M(1,0)
点评 此题是二次函数综合题,主要考查待定系数法求函数解析式,两点间的距离公式,面积的计算,解本题的关键是表示线段,难点是四边形面积的分割.

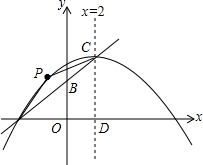 在平面直角坐标系中,A(-4,0),B(0,2),直线x=2与直线AB交于点C,与x轴交于点D,抛物线经过点A,且以C为顶点.
在平面直角坐标系中,A(-4,0),B(0,2),直线x=2与直线AB交于点C,与x轴交于点D,抛物线经过点A,且以C为顶点.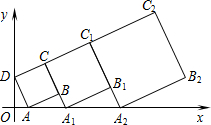 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是5×($\frac{3}{2}$)4030.
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是5×($\frac{3}{2}$)4030. 如图,抛物线y=ax2+bx+c经过点A(-3,0)、B(1,0)、C(0,3).
如图,抛物线y=ax2+bx+c经过点A(-3,0)、B(1,0)、C(0,3). 已知∠BAC=90°,四边形ADEF是正方形且边长为1,则$\frac{1}{AB}$+$\frac{1}{BC}$+$\frac{1}{CA}$的最大值为1+$\frac{\sqrt{2}}{4}$,简述理由(可列式):$\frac{1}{AB}$+$\frac{1}{BC}$+$\frac{1}{CA}$的最大值=1+$\frac{\sqrt{2}}{4}$.
已知∠BAC=90°,四边形ADEF是正方形且边长为1,则$\frac{1}{AB}$+$\frac{1}{BC}$+$\frac{1}{CA}$的最大值为1+$\frac{\sqrt{2}}{4}$,简述理由(可列式):$\frac{1}{AB}$+$\frac{1}{BC}$+$\frac{1}{CA}$的最大值=1+$\frac{\sqrt{2}}{4}$.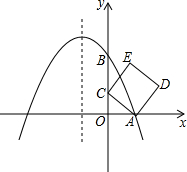 如图,在平面直角坐标系中,抛物线y=ax2+bx+2与x轴交于点A(1,0),与y轴交于点B,其对称轴是x=-1,点C是y轴上一点,其纵坐标为m,连结AC,将线段AC绕点A顺时针旋转90°得到线段AD,以AC、AD为边作正方形ACED.
如图,在平面直角坐标系中,抛物线y=ax2+bx+2与x轴交于点A(1,0),与y轴交于点B,其对称轴是x=-1,点C是y轴上一点,其纵坐标为m,连结AC,将线段AC绕点A顺时针旋转90°得到线段AD,以AC、AD为边作正方形ACED.