题目内容
5.已知:?ABCD,点G在边BC上,直线AG交对角线BD于点F、交DC延长线于点E.(1)如图(1),求证:△ABG∽△EDA;
(2)如图(2),若∠GCE=2∠ADB,AF:FE=1:2,写图中所有与AD相等的线段.
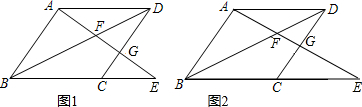
分析 (1)根据平行四边形的性质得到∠ABG=∠EDA,AB∥DE,由平行线的性质得到∠BAG=∠DEA,即可得到结论;
(2)由四边形ABCD是平行四边形,得到AD∥BC,AD=BC,根据平行线的性质得到∠ADB=∠DBC,根据三角形的外角的性质得到∠GCE=∠DBC+∠BDC,等量代换得到∠DBC=∠BDC,得到四边形ABCD是菱形,根据菱形的性质得到AB=BC=CD=AD,根据相似三角形的性质得到$\frac{AD}{BE}=\frac{AF}{EF}$=$\frac{1}{2}$,求得BC=CE,于是得到结论.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴∠ABG=∠EDA,AB∥DE,
∴∠BAG=∠DEA,
∴△ABG∽△EDA
(2)解:∵四边形ABCD是平行四边形,
∴AD=BC,
∴∠ADB=∠DBC,
∵∠GCE=2∠ADB=2∠DBC,
∵∠GCE=∠DBC+∠BDC,
∴∠DBC=∠BDC,
∴BC=CD,
∴四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵AD∥BC,
∴△ADF∽△BFE,
∴$\frac{AD}{BE}=\frac{AF}{EF}$=$\frac{1}{2}$,
∴AD=$\frac{1}{2}$BE,
∴BC=CE,
∴与AD相等的线段有AB、BC、CD、CE.
点评 本题考查了相似三角形的判定和性质,平行四边形的性质,菱形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
2.设a,b是方程x2+x-2016=0的两个实数根,则a2+2a+b的值为( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
16.在坐标系中,已知A(2,0),B(-3,-4),C(0,0),则△ABC的面积为( )
| A. | 4 | B. | 6 | C. | 8 | D. | 3 |
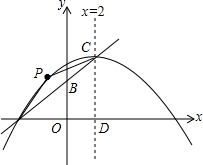 在平面直角坐标系中,A(-4,0),B(0,2),直线x=2与直线AB交于点C,与x轴交于点D,抛物线经过点A,且以C为顶点.
在平面直角坐标系中,A(-4,0),B(0,2),直线x=2与直线AB交于点C,与x轴交于点D,抛物线经过点A,且以C为顶点.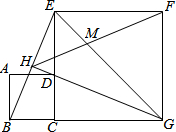 如图,正方形ABCD的边CD在正方形ECGF边CE上,DG平分∠EGC,延长GD交BE于H,EG与FH交于点M,若DC=$2-\sqrt{2}$,则GM=$\sqrt{2}$.
如图,正方形ABCD的边CD在正方形ECGF边CE上,DG平分∠EGC,延长GD交BE于H,EG与FH交于点M,若DC=$2-\sqrt{2}$,则GM=$\sqrt{2}$. 如图,点E为正方形ABCD中AD边上的动点,AB=2,以BE为边画正方形BEFG,连结CF和CE,则△CEF面积的最小值为$\frac{3}{2}$.
如图,点E为正方形ABCD中AD边上的动点,AB=2,以BE为边画正方形BEFG,连结CF和CE,则△CEF面积的最小值为$\frac{3}{2}$.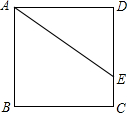 如图,已知正方形ABCD,点E在边DC上,DE=4,EC=2,则AE的长为$\sqrt{52}$.
如图,已知正方形ABCD,点E在边DC上,DE=4,EC=2,则AE的长为$\sqrt{52}$. 如图,抛物线y=ax2+bx+c经过点A(-3,0)、B(1,0)、C(0,3).
如图,抛物线y=ax2+bx+c经过点A(-3,0)、B(1,0)、C(0,3).