题目内容
15. 一个反比例函数在第二象限的图象如图所示,点A是图象上任意一点,AM⊥x轴,垂足为M,O是原点,如果△AOM的面积是3,求这个反比例函数的解析式是( )
一个反比例函数在第二象限的图象如图所示,点A是图象上任意一点,AM⊥x轴,垂足为M,O是原点,如果△AOM的面积是3,求这个反比例函数的解析式是( )| A. | y=-$\frac{3}{x}$ | B. | y=$\frac{3}{x}$ | C. | y=$\frac{6}{x}$ | D. | y=-$\frac{6}{x}$ |
分析 在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{|k|}{2}$,且保持不变.
解答 解:由题意得,k<0,$\frac{|k|}{2}$=3,
故可得:k=-6,即函数解析式为:y=-$\frac{6}{x}$.
故选D.
点评 本题考查了待定系数法求反比例函数解析式,反比例函数系数k的几何意义,注意掌握在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{|k|}{2}$,且保持不变.

练习册系列答案
相关题目
5.若|1-x|+$\sqrt{x-1}$=0,则x的取值范围是( )
| A. | x≥1 | B. | x=1 | C. | x≤1 | D. | x>1 |
20.已知点A(-3,y1),B(-2,y2),C(3,y3)都在反比例函数y=$\frac{-{m}^{2}-1}{x}$的图象上,则( )
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y3<y1<y2 | D. | y2<y1<y3 |
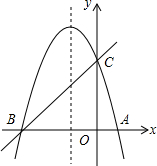 如图,已知抛物线y=ax2+bx+c(a≠0)经过A,B,C三点,点B的坐标为(-3,0),且OC=3OA,直线y=x+m经过B、C两点.
如图,已知抛物线y=ax2+bx+c(a≠0)经过A,B,C三点,点B的坐标为(-3,0),且OC=3OA,直线y=x+m经过B、C两点.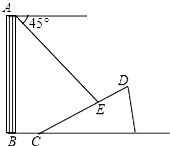 如图,一楼房AB后有一假山,山坡斜面CD与水平面夹角为30°,坡面上点E处有一亭子,测得假山坡脚C与楼房水平距离BC=10米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.求楼房AB的高(结果保留根号).
如图,一楼房AB后有一假山,山坡斜面CD与水平面夹角为30°,坡面上点E处有一亭子,测得假山坡脚C与楼房水平距离BC=10米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.求楼房AB的高(结果保留根号).