题目内容
20.已知点A(-3,y1),B(-2,y2),C(3,y3)都在反比例函数y=$\frac{-{m}^{2}-1}{x}$的图象上,则( )| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y3<y1<y2 | D. | y2<y1<y3 |
分析 先根据反比例函数的解析式判断出函数的增减性,再由各点横坐标的值判断出各点所在的象限,进而可得出结论.
解答 解:∵反比例函数y=$\frac{-{m}^{2}-1}{x}$中,-m2-1<0,
∴函数图象的两个分支分别位于二四象限,且在每一象限内y随x的增大而增大.
∵-3<-2<0,3>0,
∴点A、B位于第二象限,点C位于第四象限,
∴0<y1<y2,y3<0,
∴y3<y1<y2.
故选C.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
10.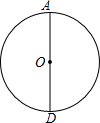 如图,AD为⊙O直径,作⊙O的内接正三角形ABC,作法错误的是( )
如图,AD为⊙O直径,作⊙O的内接正三角形ABC,作法错误的是( )
 如图,AD为⊙O直径,作⊙O的内接正三角形ABC,作法错误的是( )
如图,AD为⊙O直径,作⊙O的内接正三角形ABC,作法错误的是( )| A. | 作OD的中垂线,交⊙O于B、C,连结AB,AC | |
| B. | 以D点为圆心,OD长为半径作圆弧,交圆于点B,C,连结AB,BC,CA | |
| C. | 以A点为圆心,AO长为半径作圆弧,交圆于点E,F,分别以E,F为圆心作圆弧,交圆于不同于点A的两点B,C,连结AB,BC,CA | |
| D. | 作AD的中垂线,交⊙O于B、C,连结AB,AC |
11.已知一元二次方程x2-5x+3=0,则该方程根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
15. 一个反比例函数在第二象限的图象如图所示,点A是图象上任意一点,AM⊥x轴,垂足为M,O是原点,如果△AOM的面积是3,求这个反比例函数的解析式是( )
一个反比例函数在第二象限的图象如图所示,点A是图象上任意一点,AM⊥x轴,垂足为M,O是原点,如果△AOM的面积是3,求这个反比例函数的解析式是( )
 一个反比例函数在第二象限的图象如图所示,点A是图象上任意一点,AM⊥x轴,垂足为M,O是原点,如果△AOM的面积是3,求这个反比例函数的解析式是( )
一个反比例函数在第二象限的图象如图所示,点A是图象上任意一点,AM⊥x轴,垂足为M,O是原点,如果△AOM的面积是3,求这个反比例函数的解析式是( )| A. | y=-$\frac{3}{x}$ | B. | y=$\frac{3}{x}$ | C. | y=$\frac{6}{x}$ | D. | y=-$\frac{6}{x}$ |
12.81的算术平方根是( )
| A. | 9 | B. | ±9 | C. | 3 | D. | ±3 |
9.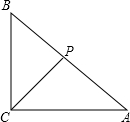 已知:Rt△ABC中,∠ACB=90°,CP平分∠ACB交边AB于点P,点D在边AC上.
已知:Rt△ABC中,∠ACB=90°,CP平分∠ACB交边AB于点P,点D在边AC上.
(1)如果PD∥BC,求证:AC•CD=AD•BC;
(2)如果∠BPD=135°,求证:CP2=CB•CD.
 已知:Rt△ABC中,∠ACB=90°,CP平分∠ACB交边AB于点P,点D在边AC上.
已知:Rt△ABC中,∠ACB=90°,CP平分∠ACB交边AB于点P,点D在边AC上.(1)如果PD∥BC,求证:AC•CD=AD•BC;
(2)如果∠BPD=135°,求证:CP2=CB•CD.
10.有甲、乙两个不透明的袋子中装着只有颜色不同的小球,甲袋中有两个红球,乙袋中有一个红球,一个白球,从两个袋中各摸出一个球,则两个球都是红球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |