题目内容
6.(1)先化简,再求值:2a(a+2b)-(a+2b)2,其中a=-1,b=$\sqrt{3}$.(2)解方程:$\frac{2}{x+1}$=$\frac{1}{x-1}$.
分析 (1)原式利用单项式乘以多项式,完全平方公式化简,去括号合并得到最简结果,把a与b的值代入计算即可求出值;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=2a2+4ab-a2-4ab-4b2=a2-4b2,
把a=-1,b=$\sqrt{3}$代入得,原式=(-1)2-4×($\sqrt{3}$)2=1-12=-11;
(2)去分母得:2x-2=x+1,
解得:x=3,
经检验x=3是分式方程的解.
点评 此题考查了解分式方程,以及整式的加减-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16.下列运算中,正确的是( )
| A. | a2+a3=a5 | B. | $\sqrt{4}$=±2 | C. | a2•a3=a5 | D. | (2a)3=6a3 |
17.为执行中央“节能减排,美化环境,建设美丽新农村”的国策,我市某村计划建造A、B两种型号的沼气池共20个,以解决该村所有农户的燃料问题.两种型号沼气池的占地面积、使用农户数及造价见下表:
已知可供建造沼气池的占地面积不超过370m2,该村农户共有498户.
(1)满足条件的方案共有哪几种?写出解答过程.
(2)通过计算判断,哪种建造方案最省钱?造价最低是多少万元?
| 型号 | 占地面积(m2/个) | 使用农户数(户/个) | 造价(万元/个) |
| A | 15 | 18 | 2 |
| B | 20 | 30 | 3 |
(1)满足条件的方案共有哪几种?写出解答过程.
(2)通过计算判断,哪种建造方案最省钱?造价最低是多少万元?
11.已知一元二次方程x2-5x+3=0,则该方程根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
15. 一个反比例函数在第二象限的图象如图所示,点A是图象上任意一点,AM⊥x轴,垂足为M,O是原点,如果△AOM的面积是3,求这个反比例函数的解析式是( )
一个反比例函数在第二象限的图象如图所示,点A是图象上任意一点,AM⊥x轴,垂足为M,O是原点,如果△AOM的面积是3,求这个反比例函数的解析式是( )
 一个反比例函数在第二象限的图象如图所示,点A是图象上任意一点,AM⊥x轴,垂足为M,O是原点,如果△AOM的面积是3,求这个反比例函数的解析式是( )
一个反比例函数在第二象限的图象如图所示,点A是图象上任意一点,AM⊥x轴,垂足为M,O是原点,如果△AOM的面积是3,求这个反比例函数的解析式是( )| A. | y=-$\frac{3}{x}$ | B. | y=$\frac{3}{x}$ | C. | y=$\frac{6}{x}$ | D. | y=-$\frac{6}{x}$ |
16.小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为95分、80分、90分,若依次按照60%、30%、10%确定成绩,则小王的成绩是( )
| A. | 85.5分 | B. | 90分 | C. | 92分 | D. | 265分 |
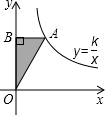 如图,点A是反比例函数y=$\frac{k}{x}$(k≠0)图象上一点,AB⊥y轴,垂足为点B,S△AOB=3,则以下结论:
如图,点A是反比例函数y=$\frac{k}{x}$(k≠0)图象上一点,AB⊥y轴,垂足为点B,S△AOB=3,则以下结论: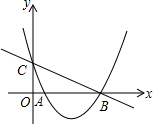 如图,已知抛物线y=ax2-5ax+2(a≠0)与y轴交于点C,与x轴交于点A(1,0)和点B.
如图,已知抛物线y=ax2-5ax+2(a≠0)与y轴交于点C,与x轴交于点A(1,0)和点B.